- Ілюстрації проблеми
- Комп’ютерні дробові числа
- IEEE 754
- IEEE 754 в програмуванні
- FP8
- Підсумок
- Додатки
- Посилання
- Виноски
Floating point numbers – числа із рухомою крапкою1. Давайте розглянемо, як їх представляють в комп’ютерах і які це має наслідки для обчислень.
Ілюстрації проблеми
Рекурентна послідовність Мюллера
Перш ніж перейти до подробиць, спробуйте обчислити таку рекурентну послідовність, де всі змінні – floating point2, з допомогою будь-якої мови програмування – Python, C, C++, Rust, Lua тощо:
fn(x, y) := 108 - (815 - 1500/y)/x
v_0 = 4
v_1 = 4.25
v_i = fn(v_{i-1}, v_{i-2})
Це так-звана рекурентна послідовність Мюллера (J-M. Muller’s Recurrence). Детальніше про неї, а також – про інші проблеми з комп’ютерними обчисленнями з рухомою крапкою (floating point) – див. “How Futile are Mindless Assessments of Roundoff in Floating-Point Computation?”3
Ця послідовність збіжна, її границя, враховуючи, що:
\[v_i = 5 – \frac 2 { 1 + (5/3)^i } = 8 – 15/v^{i–1},\]дорівнює 5. Що ж дають обчислення? Візьмемо такий код:
#include <iostream>
#include <cstdlib>
#include <iomanip>
double fn(double x, double y){
return 108.0 - (815.0 - 1500.0/y)/x;
}
int main() {
size_t iters = 0;
std::cout << std::setprecision(15);
std::cout << "v_i:\n";
const double epsilon = 1E-7;
double v_i_2 = 4; // v_0 = 4
double v_i_1 = 4.25; // v_1 = 4.25
double v_i = fn(v_i_1, v_i_2);
while( std::abs(v_i - v_i_1) > epsilon ) {
std::cout << v_i << std::endl;
v_i_2 = v_i_1;
v_i_1 = v_i;
v_i = fn(v_i_1, v_i_2);
++iters;
}
std::cout << "v_i = " << v_i << ", for "
<< iters << " iterations, local error: "
<< std::abs(v_i - v_i_1) << std::endl;
return 0;
}
Виконавши, наприклад, на Godbolt.org, отримаємо наступне.
Результат:
v_i: 4.47058823529412 4.64473684210522 4.77053824362508 4.85570071256856 4.91084749866063 4.94553739553051 4.966962408041 4.98004220429301 4.98790923279579 4.99136264131455 4.96745509555227 4.42969049830883 -7.81723657845932 168.939167671065 102.039963152059 100.09994751625 100.004992040972 100.000249579237 100.00001247862 100.000000623922 100.000000031196 v_i = 100.00000000156, for 21 iterations, local error: 2.96360127549633e-08
Перш, ніж розкривати спойлер – спробуйте самостійно! Чому так виходить, розглянуто у згаданій статті, якщо коротко, похибка заокруглення змушує збігатися до іншого, тут – невірного, розв’язку певного рівняння. Конкретна ситуація, звичайно, створена штучно, але – правдоподібна, в реальних обчисленнях таке трапляється, однак, розібратися там може бути складніше.
Десяткова аналогія
Отже, з комп’ютерними числами з рухомою крапкою не все просто. Щоб краще відчути це, розглянемо простіший приклад. Нехай є десятковий калькулятор4, який може зберігати чотири десяткові цифри. Виконаємо просте обчислення двічі, використовуючи різний порядок операцій і зберігаючи в проміжному результаті не більше чотирьох цифр:
1.000 / 3.000 * 3.000 = 0.333 * 3.000 = 0.999
3.000 / 3.000 * 1.000 = 1.000 * 1.000 = 1.000
Через скінчену кількість цифр, результат залежить від порядку операцій. При тому, навіть на такому простому прикладі видно – порівнювати числа з рухомою крапкою за допомогою простої рівності – нерозумно5. З точки зору машинних обчислень, обидва результати вірні настільки, наскільки машині вистачило точності. Тому порівнювати floating point змінні a та b потрібно так:
\[| a - b | < \epsilon,\]де \(\epsilon\) – величина похибки. Її вибір – окрема тема, до якої ще повернемося.
Класичний приклад цієї проблеми з популярних текстів:
0.1+0.2-0.3 = 5.551115123125783e-17.
ОК, з порівнянням зрозуміло. А як із обчисленнями? Обчислимо на такому калькуляторі формулу:
\[r = a^2 - b^2.\]для \(a = 12.35\) і \(b = 12.34\). Пам’ятаючи, що всі проміжні результати обмежуються чотирма цифрами, та відкидаючи зайві цифри на кожному кроці, отримуємо: $r = 0.3$ Це значення дуже відрізняється від правильного, \(0.2469\). Як можна виправити це? Потрібно скористатися формулою, яка не змушуватиме віднімати близькі один до одного числа:
\[r = (a - b) (a + b).\]Для наочності, підсумуємо всі обчислення в табличці:
| \(a^2\) | \(b^2\) | \(a^2-b^2\) | \((a - b)\) | \((a + b)\) | \((a - b) (a + b)\) | |
|---|---|---|---|---|---|---|
| Точно | 152.5225 | 152.2756 | 0.2469 | 0.01 | 24.69 | 0.2469 |
| На калькуляторі, обрізано | 152.5 | 152.2 | 0.3 | 0.01 | 24.69 | 0.246 |
| Похибка, % | 0.01% | 0.05% | 21.5% | 0% | 0% | 0.4% |
| На калькуляторі, заокругл. | 152.5 | 152.3 | 0.2 | 0.01 | 24.69 | 0.247 |
| Похибка, % | 0.01% | 0.02% | 19.0% | 0% | 0% | 0.04% |
Похибка6 – відносно точного значення, яке ми тут знаємо. Як працювати, коли точне значення невідоме – а так буде в абсолютній більшості практичних випадків, розглянемо в майбутньому.
Як видно, різниця між двома способами обчислити формулу на комп’ютері із фіксованою кількістю цифр у представленні чисел – фантастична. Наступне Питання, найкраща отримана похибка, \(0.04\%\), наскільки вона хороша? Порівнявши точне та отримане значення, бачимо, що вона ідеальна – навіть візуально видно, що краще наблизитися неможливо. Різниця між точним та отриманим значенням дорівнює \(0.0001\), менше половини останньої значущої цифри.
Важливо розуміти, що похибка, за наївного обчислення, не з’явилася під час віднімання – тут лише проявилася похибка, отримана під час піднесення до квадрату. Оскільки квадрати були близькими, похибка, залишаючись малою за абсолютною величиною, почала складати велику відносно частку результату – вона своєрідно підсилилася.
Ремарка: чи завжди \(r = (a - b) (a + b)\) буде обчислюватися точніше, ніж \(r = a^2 - b^2\)? Взагалі кажучи, ні. Якщо одне із a чи b, багато більше за інше, друга формула дасть трохи точніший результат. Перевірити це можна, побудувавши аналогічну табличку. Однак, перша захищена від катастрофічної втрати точності, а друга – ні. Тому, перша, в загальному випадку, є кращим варіантом.
’‘Array ordering and naive summation’’ – приклад, коли переставляння порядку підсумовування дозволяє отримати практично будь-який результат. Але див., наприклад, лема Штербенца (Sterbenz lemma) та Алгоритм Кехена (Kahan summation).
Комп’ютерні дробові числа
Побачивши, що комп’ютерні числа з рухомою крапкою, (floating point numbers), не такі прості, як могло б здатися та потребують уважності, давайте розглянемо, а які ж вони – як насправді представляються в комп’ютерах.
Коротке пояснення деяких загальних термінів
Цей текст є частиною більшого курсу, тому вважається, що деякі потрібні поняття відомі читачам. З іншого боку, щодо деяких є циклічні залежності – щоб розуміти А, потрібно розуміти Б, а щоб розуміти Б – потрібно розуміти А. Щоб спростити читачам розуміння подальшого тексту, нагадаємо коротко основні поняття, використані в ньому.
Необхідною передумовою є:
- Розуміння понять байт, біт.
- Хоча б базове володіння двійковою системою.
- Корисним буде розуміння доповнювального коду.
В принципі, все це можна засвоїти з нуля за один вечір. Окремо про розуміння десяткової арифметики, аж по піднесення до степені, не будемо говорити.
Важливо розуміти, що процесори (CPU) реалізовують певну систему команд – instruction set architecture, ISA, яка включає:
- Машинні команди, які буде виконувати процесор.
- Вони кодуються певною послідовністю біт.
- Для спрощення використання людьми, машинним командам у відповідність ставляться певні текстові мнемоніки – набір мнемонік, разом із всілякими службовими засобами, формує асемблер для конкретної ISA.
- Регістри.
- Регістри – це такі своєрідні “змінні”, що є частиною процесора.
- Багато команд процесора працюють над вмістом регістрів.
- Регістри можна поділити на регістри загального використання та спеціалізовані регістри.
- Спеціалізовані регістри, зокрема, використовуються для керування процесором та визначення його стану.
- Часто процесори обладнанні окремими регістрами для floating-point чисел.
- Способи адресації.
- Пам’ять сучасних комп’ютерів – пронумерована послідовність байт.
- Спосіб адресації – спосіб задати цю адресу.
Інтринсики – псевдо-функції компіляторів, це можливість в коді, скажімо C чи C++, використати певні машинні команди чи інші засоби, не задані стандартом, але важливі для конкретної платформи.
Частиною ISA є переривання. Якщо відбувається якась подія, зовнішня – від зовнішніх пристроїв, чи внутрішня – через помилки в коді, чи, ось, виключні ситуації floating point, процесор призупиняє виконання поточного коду і стрибає до наперед визначеного коду – обробника переривань (ISR). Зазвичай, керуванням цією машинерією здійснюється операційною системою, яка, за потреби, може транслювати у щось видиме прикладним програмам – сигнали, structured exceptions Windows тощо, які runtime-кодом конкретних мов програмування можуть транслюватися у засоби цих мов, таких як виключення С++ чи Python.
“Слова” x86, ARM, RISC-V – це назви популярних ISA, чи, точніше, сімейств ISA.
Двійкові дробові числа
Там, де це може призвести до плутанини, будемо позначати двійкові числа літерою b, десяткові – літерою d: \(5d = 101b.\) Якщо з контексту однозначно зрозуміло, заради лаконічності ці літери можуть пропускатися.
Розпочнемо з дробів в десятковій системі числення:
\[123.456 = 1 \cdot 100 + 2 \cdot 10 + 3 \cdot 1 + \frac 4 {10} + \frac 5 {100} + \frac 6 {1000},\]Щоб підкреслити, що основа цієї системи числення – десять, перепишемо так:
\[123.456 = 1 \cdot 10^2 + 2 \cdot 10^1 + 3 \cdot 10^0 + 4 \cdot 10^{-1} + 5 \cdot 10^{-2} + 6 \cdot 10^{-3}.\]В двійковій системі ввести дробові числа можна аналогічно:
\[101.0101b = 1\cdot 4d + 0\cdot 2d + 1\cdot 1d + \frac 0 {2d} + \frac 1 {4d} + \frac 0 {8d} + \frac 1 {16d} = 5.3125d.\]Ремарка: не всі скінчені дроби десяткової будуть скінченими дробами двійкової, але зворотне невірне – будь-який скінчений двійковий дріб може бути записаний як скінчений десятковий дріб. Приклад: \(0.7d = 0.10110011(0011)b,\) де в дужках – період.
Якщо взяти 52 біти із цього дробу (чому саме стільки, стане зрозуміліше трохи пізніше): \(0.1011001100110011001100110011001100110011001100110011b,\) це відповідатиме десятковому дробу \(0.6999999999999999555910790149937383830547332763671875\) – різниця з вихідним числом, 0.7, буде суттєвою десь із 17-ї десяткової цифри після крапки.
Тобто, частину десяткових дробів неможливо записати скінченою кількістю двійкових цифр.
Зазвичай, ми використовуємо наукову нотацію – замість \(123.456\) пишемо: \(1.23456\cdot 10^{2},\) перетворюючи так, щоб перед крапкою була лише одна цифра, відмінна від нуля – вона може набувати дев’ять різних значень.
Аналогічний запис можна запропонувати і для двійкових чисел:
\[101.0101b = 1.010101b\cdot 10b^{10b} = 1.010101b\cdot 2d^{2d}.\]Зауважте, що перед крапкою може стояти лише одна не нульова цифра – 1.
Власне, це і є запис з рухомою крапкою у двійковій системі. Степінь, до якої підносять основу, називають експонентою.
Представлення в комп’ютері
Базові типи змінних, такі як int чи double в C/C++/Java/тощо, мають фіксований розмір – вони займають фіксовану кількість бітів. Якщо ми хочемо записати двійкове дробове число із рухомою крапкою, на що нам потрібно розподілити ці біти? Врахуємо такі фактори:
- Оскільки перед крапкою завжди 1, її можна не зберігати.
- Доповнювальний код для floating point чисел застосовувати нераціонально7.
- Число може бути і додатнім і від’ємним.
- Степінь теж може бути і додатною – для представлення великих чисел, (більших чи рівних 2) і від’ємною – для малих, менших, ніж 1.
Тоді, нам потрібно зберегти наступну інформацію:
- знак числа,
- його дробову частину, без одинички перед крапкою – мантису,
- знак експоненти,
- значення експоненти.
З технічних причин та для більшої гнучкості, знак експоненти не зберігають, а вводять додаткову характеристику8 – зсув, bias, вважаючи, що якщо в експоненті збережено значення E, то дробова частина множиться на:
\[2^{\mathrm{E} - \mathrm{bias}}.\]Таким чином, нам потрібен один біт для знаку, \(N_m\) для мантиси і \(N_E\) для експоненти. Для певного спрощення9, прийнято записувати ці біти в такій послідовності, зліва направо, від старших – більш значущих (MSB – most significant bit) до молодших – менш значущих (LSB – least significant bit):
s e...ee m...mm
де s – біт знаку, e – біти експоненти, m – біти мантиси.
Спеціальні значення
Infinity
За наївного підходу, є певне максимальне за модулем число, яке можна записати за допомогою форматів, розглянутих вище: \(1.11....1b \cdot 2d^{1...11b}\). А що робити, якщо результат більший за це число? Можна повідомляти про помилку. Однак, часто зручно вважати, що всі результати більше певного числа – безмежність.
Давайте домовимося, що число, для якого експонента – максимальна, всі одинички, а мантиса – нуль, буде означати нескінченість, додатну чи від’ємну, в залежності від знаку: \(\pm \infty\). Будь-який результат, який більший за модулем, ніж число10, записане як: s 1...10 1...11, де пробілами розділено біт знаку, експоненти та мантиси, будемо зберігати як безмежність – число, із представленням s 1...11 0...00.
Використання безмежностей, із звичними правилами операцій над ними, дозволяє отримати, принаймні, правильну границю результату.
NaN
Не завжди результат операції можна записати як floating point число – наприклад, \(0/0\), \(\sqrt{-1}\), \(\infty - \infty\) тощо.
Домовимося, що число із максимальною (всі одинички) експонентою та не нульовою мантисою це так-звані не-числа, Not a Number (NaN) – представлення для невірного результату, такого, що неможливо записати.
Використовуючи біти мантиси, можна закодувати подробиці помилки, або ще якусь корисну інформацію (див. далі NaN-boxing) – це так-зване корисне навантаження, payload.
Є помилки, про які потрібно повідомляти негайно, а є такі, що дозволяють продовжувати обчислення. Перші можна представити як signaling NaN (sNaN), другі – як quiet NaN (qNaN). Якщо в обчисленнях виникає quiet NaN, вони продовжуються, а поява signaling NaN спричиняє виключення абощо – але обробник може перетворити його на quiet.
Реалізації сильно відрізняються, але рекомендується11 використання мантиси
0m...mm, де хоча б один бітmне дорівнює нуль для signaling NaN і1m...mmдля quiet NaN.
Будь-яка операція над NaN дає NaN. Виняток – тривіальні операції, наприклад \(1^{NaN}\), яка мала б давати 1, однак, поведінка фактичних реалізацій відрізняється.
Ще одна особливість NaN – вони не порівнянні навіть самі із собою. Будь-яка операція порівняння, окрім “!=”: “==”, “>=”, “>”, “<=”, “<” із NaN завжди повертає false, а “!=” – завжди true.
Нуль
Окремо, домовимося, що коли мантиса і експонента дорівнюють нулю – це просто нуль. Їх є два – +0 і -0.
Приклад – FP5
Описане вище – трохи абстрактне. Давайте розглянемо конкретний простий приклад – п’яти-бітове floating point число, де два біти виділено для мантиси, і два – для експоненти. Візьмемо bias = 1 та 2. П’ять біт – це \(2^5 = 32\) комбінацій, давайте запишемо їх всіх:
| Двійкове | Десяткове, bias = 1 | Десяткове, bias = 2 |
|---|---|---|
| 0 00 00 | 0.00 | 0.00 |
| 0 00 01 | 0.625 | 0.3125 |
| 0 00 10 | 0.75 | 0.375 |
| 0 00 11 | 0.875 | 0.4375 |
| 0 01 00 | 1.0 | 0.50 |
| 0 01 01 | 1.25 | 0.625 |
| 0 01 10 | 1.5 | 0.75 |
| 0 01 11 | 1.75 | 0.875 |
| 0 10 00 | 2.0 | 1.00 |
| 0 10 01 | 2.5 | 1.25 |
| 0 10 10 | 3.0 | 1.50 |
| 0 10 11 | 3.5 | 1.75 |
| 0 11 00 | \(+\infty\) | \(+\infty\) |
| 0 11 01 | sNaN | sNaN |
| 0 11 10 | qNaN | qNaN |
| 0 11 11 | qNaN | qNaN |
| 1 00 00 | -0.0 | -0.0 |
| 1 00 01 | -0.625 | -0.3125 |
| 1 00 10 | -0.75 | -0.375 |
| 1 00 11 | -0.87 | -0.4375 |
| 1 01 00 | -1.0 | -0.50 |
| 1 01 01 | -1.25 | -0.625 |
| 1 01 10 | -1.5 | -0.75 |
| 1 01 11 | -1.75 | -0.875 |
| 1 10 00 | -2.0 | -1.00 |
| 1 10 01 | -2.5 | -1.25 |
| 1 10 10 | -3.0 | -1.50 |
| 1 10 11 | -3.5 | -1.75 |
| 1 11 00 | \(-\infty\) | \(-\infty\) |
| 1 11 01 | sNaN | sNaN |
| 1 11 10 | qNaN | qNaN |
| 1 11 11 | qNaN | qNaN |
Бачимо, що:
- Найменше за модулем число, відмінне від нуля – 0.625.
- Найбільше скінчене – 3.5.
- Віддаль між 1.0 та наступним числом – 0.25.
- Як ми побачимо в майбутньому, це важлива характеристика floating point формату.
- Для деяких чисел із таблички, щоб записати їх точно, потрібно 4 значущих десяткових цифри.
- Однак, фактично, всі ці числа можна пронумерувати двома десятковими цифри, оскільки їх лише 12.
- Це можна зробити, наприклад, для bias = 1, так : 0.0, 0.62, 0.75, 0.9, 1.0, 1.25, 1.5, 1.8, 2, 2.5, 3.0, 3.5.
- Тому, фактично, значущих десяткових цифр – дві.
- Можна означити, що кількість значущих цифр – така кількість, якої достатньо, щоб можна було перетворити число в стрічку і назад без втрат.
Зобразимо додатні числа12 із таблички на числовій вісі:

З цього рисунку можна зробити два висновки:
- Більші числа представляються менш точно.
- Наприклад, тут, між 1 і 2 крок – 0.25, а між 2 і 3.5 – 0.5.
- Ця величина називається “Unit in the last place” (ULP) – ціна останнього, наймолодшого, двійкового розряду.
- Тобто, якщо точне значення знаходиться між 3.0 та 3.5, воно перетвориться до 3.0 або 3.5, і, за правильного заокруглення, похибка складатиме 0.5/2 = 0.25, А якщо між 1.0 і 1.25 – лише 0.25/2 = 0.125, в обох випадках – до половини ULP.
- Відповідно, для досягнення максимальної точності, бажано, щоб числа, які циркулюють в змінних, були близькі до 1.
- Між 0 і 0.625 немає представимих чисел. Тобто, числа в цьому інтервалі будуть заокруглятися або до нуля, або до 0.625.
- Це дуже помітна втрата точності, особливо враховуючи, що в багатьох обчисленнях результати знаходяться в цьому інтервалі.
- Заокруглення до нуля в таких випадках називають втратою точності, або, англійською, underflow.
- Стандартне виключення С++, std::underflow_error призначене повідомляти про таку проблему.
Першу проблему можна вирішити або збільшенням розміру floating point числа – використовувати формат із більшою кількістю біт, або – оскільки це часто важко, переписуючи формули так, щоб числа залишалися малими.
Другу проблему теж можна вирішувати, намагаючись “тримати” проміжні значення в інтервалі між одиницею і двійкою. Але, враховуючи велику потребу і наявність технічної нагоди, існує більш загальне вирішення.
Денормалізовані числа
Щоб заповнити дірку між 0 та наступним представими значенням, 0.625, для розглянутого раніше FP5, скористаємося наступним трюком. Нехай, якщо експонента дорівнює нулю, вважатимемо:
- Перед десятковою крапкою неявно знаходиться нуль, а не одиниця.
- Bias беремо меншим на одиницю – позначатиму його dn-bias.
- Для розглянутих FP5, dn-bias = 0 та dn-bias = 1.
| Двійкове | Десяткове, bias = 1 | Десяткове, bias = 2 |
|---|---|---|
| 0 00 00 | 0.00 | 0.00 |
| 0 00 01 | 0.25 | 0.125 |
| 0 00 10 | 0.50 | 0.25 |
| 0 00 11 | 0.75 | 0.375 |
| 0 01 00 | 1.00 | 0.50 |
 |
|---|
| Зверху – без денормалізованих чисел, внизу – з денормалізованими. |
При цьому, втрата точності все ще відбувається, але вона – поступова (gradual underflow). Такі числа називають денормалізованими числами. В англійській мові зараз рекомендується вживати термін subnormal numbers, але denormalized numbers все ще широко використовується13. Нуль, зазвичай, не вважається денормалізованим числом.
IEEE 754
До початку 80-х, floating point типи представлялися різними архітектурами процесорів (ISA) різними способами, зазвичай – несумісними між собою, хоч і дуже схожими. Це було проблемою, тому, після довгих дискусій між ключовими виробниками, в 1985 було прийнято IEEE Standard for Floating-Point Arithmetic (IEEE 754), який оновлювався в 2008 та 2019.
Ремарка: стандартизація тривала з 1977, цікавою є жорстка дискусія між Intel i DEC – останні не вірили в адекватність підходу із денормалізованими числами, зокрема, в можливість реалізувати їх ефективно. Інтел реалізував їх в своєму 8087, але, природно, не хотіли ділитися таємницею – як саме. Тому, взяли floating point плату DEC VAX із їх floating point арифметикою та замінили на плату, що реалізовувала IEEE-арифметику, залишаючись сумісною у всьому решта. Це допомогло. Спроба довести теоретичну дефективність такого підходу, зроблена DEC, теж дала протилежні результати, це добило опір. Джерела: “IEEE 754: An Interview with William Kahan” та An Interview with the Old Man of Floating-Point – спогади про нього, (це головний натхненник та розробник формату).
Однак, робота з денормалізованими числами все ще, зазвичай, повільна. Детальніше див., наприклад, відповідь на запитання: '’Why are denormal floating-point values slower to handle?’’.
Формат FP5, який ми розглядали вище, створений згідно принципів, визначених в IEEE 754. Стандарт визначає декілька базових двійкових форматів, формати для обміну інформацією, десяткові формати та розширені типи. Далі ми коротко розглянемо лише основні двійкові формати.
Стандарт також визначає операції над цими числами, правила заокруглення, опціональні математичні функції з вимогами до їх поведінки, якщо вони реалізовані та набір виключних ситуацій, про які слід повідомляти.
Основні двійкові стандарти
Стандартизовано наступні формати:
 |
|---|
| Binary16 – half precision, bias = 15. Називатимемо його надалі FP16. Зображення з вікі. |
 |
| Binary32 – single precision, bias = 127. Називатимемо його надалі FP32 Зображення з вікі. |
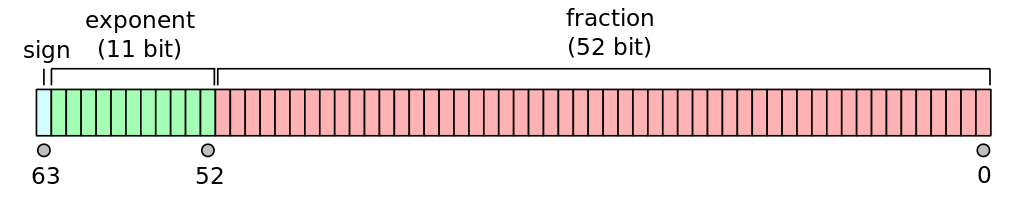 |
| Binary64 – double precision, bias = 1023. Називатимемо його надалі FP64. Зображення з вікі. |
 |
| Binary128 – quadruple precision, bias = 16383, FP128. Зображення з вікі. |
 |
| Binary128 – octuple precision, bias = 262143, FP256. Зображення з вікі. |
 |
| Binary80 – приклад extended precision формату, 80-бітовий формат співпроцесорів x87, bias = 16383 (FP80). Сам по собі не є частиною стандарту, але такі типи ним дозволяються. У явному вигляді зберігає одиницю перед десятковою крапкою. Зображення з вікі. |
Загальні властивості цих типів (всі числа в табличці наведені за модулем, мінімальні значення – мається на увазі, мінімальні не нульові):
| Тип | Максимальне скінчене | Наступне після 1 | мінімальне нормальне | мінімальне денормалізоване | значущих десяткових цифр |
|---|---|---|---|---|---|
| Binary16 | 65 504 | \(1.0009765625 \approx 1 + 10^{-3}\) | \(\approx 6.10 \cdot 10^{−5}\) | \(\approx 5.96 \cdot 10^{−8}\) | \(\approx 3.3\) |
| Binary32 | \(\approx 3.403 \cdot 10^{38}\) | \(\approx 1+ 1.2\cdot 10^{-7}\) | \(\approx 1.175 \cdot 10^{−38}\) | \(\approx 1.401 \cdot 10^{-45}\) | \(\approx 7.2\) |
| Binary64 | \(\approx 1.798 \cdot 10^{308}\) | \(\approx 1 + 2.2\cdot 10^{-16}\) | \(\approx 2.225 \cdot 10^{−308}\) | \(\approx 4.941 \cdot 10^{-324}\) | \(\approx 15.95\) |
| Binary128 | \(\approx 1.190 \cdot 10^{4932}\) | \(\approx 1 + 1.9\cdot 10^{-34}\) | \(\approx 3.362 \cdot 10^{-4932}\) | \(\approx 6.475 \cdot 10^{-4966}\) | \(\approx 34.0\) |
| Binary256 | \(\approx 1.611 \cdot 10^{78913}\) | \(\approx 1 + 9.0\cdot 10^{-72}\) | \(\approx 2.482 \cdot 10^{-78913}\) | \(\approx 2.248 \cdot 10^{-78984}\) | \(\approx 71.3\) |
| Binary80 | \(\approx 1.18 \cdot 10^{4932}\) | \(\approx 1 + 1.1\cdot 10^{-19}\) | \(\approx 3.36 \cdot 10^{-4932}\) | \(\approx 3.65 \cdot 10^{-4951}\) | \(\approx 19.0\) |
Віддаль від 1 до наступного числа, яке можна представити – зручна характеристика числа з рухомою крапкою. Взагалі кажучи, вона помітно корисніша на практиці за максимальне чи мінімальне значення. Її називають епсилон.
Кількість десяткових цифр – \(\log_{10} ( 2^{\mathrm{mantisaBits} + 1} )\).
Використано традиційний запис, коли нуль, явно записаний в кінці, означає значущу цифру – наприклад, число \(1.2015...\) із точністю дві цифри після крапки записується як \(1.20\) – цей нуль означає, що похибка не більша одиниці на місці цього розряду числа.
Binary16 (FP16) може зберігати числа між 0 та 2046 точно, між 2047 і 4094 – цілі числа заокругляться вниз до парних тощо.
Binary32 (FP32) зберігає точно цілі числа14 між 0 та \(16 777 216 = 2^{24}\).
Binary64 зберігає точно цілі числа між 0 та \(9 007 199 254 740 992 = 2^{53}\)
При тому, арифметичні операції над цілими числами, збереженими в форматі IEEE 754 відбувається точно, без похибок заокруглення абощо, поки всі проміжні результати знаходяться в межах цих інтервалів.
 |
|---|
| Точність представлення чисел FP32 i FP64. Зображення з вікі. |
Заокруглення
Одна із задач цього стандарту – відтворюваність обчислень. Якщо певна реалізація – апаратна чи програмна, дотримується стандарту, результати будь-яких обчислень на ній мають збігатися із результатами інших реалізацій, що відповідають стандарту. Ключовою частиною цього є правила заокруглення.
Цікаво, що іншою задачею була максимальна простота для не експертів у чисельних обчислення – мінімізація проблем, яким була присвячена перша частина цієї глави. Популярні до стандарту типи часто були “капризнішими”.
Стандарт визначає п’ять режимів заокруглення, які діляться на дві категорії.
Перша – заокруглення до найближчого:
- Заокруглення до найближчого. Якщо результат по середині – до парного.
- Це розумна поведінка за замовчуванням – забезпечує повільне зростання похибки. Зокрема, не спричиняє систематичної похибки (bias). Крім того, замість лінійно, похибка буде поводитися як у одномірному випадковому блуканні – зростатиме пропорційно квадратному кореню з кількості операцій.
- Заокруглення до найближчого. Якщо результат по середині – заокруглювати від нуля, або до безмежності із тим самим знаком, що й вихідне число.
- Не спричиняє систематичної похибки за, приблизно, рівної кількості додатних та від’ємних чисел, але спричиняє для чисел із одним знаком. Може бути ефективніше реалізованим. Іноді називають комерційним заокругленням – часто використовується для цін.
Друга – напрямлені заокруглення:
- Заокруглення до нуля. Іншими словами – обрізання до потрібної кількості цифр (truncation).
- Заокруглення до \(+\infty\) – вверх (ceiling).
- Заокруглення до \(-\infty\) – вниз (floor).
Заокруглення до плюс чи мінус безмежності корисні для інтервальних обчислень – для визначення інтервалу, в який може потрапляти результат. Обрізання просте в реалізації.
Виключення
Стандарт IEEE 754 визначає виключні ситуації, які можуть відбуватися під час обчислень:
- Invalid operation (некоректна операція) – математично невірна дія, наприклад, квадратний корінь з -1. Зазвичай, результат – NaN.
- Division by zero (ділення на нуль) – в сучасному стандарті, будь-яка операція, яка дає в результаті добре визначену безмежність – ділення на нуль, логарифм нуля тощо. Природно, результатом її є безмежність.
- Overflow (переповнення) – результат є скінченим, але завеликим, щоб його можна було представити у відповідному типі з рухомою крапкою. Зазвичай, повертає безмежність, але із направленими режимами заокруглення можуть бути нюанси.
- Underflow (втрата точності) – результат не нульовий, але менший, ніж можна представити нормальними числами. Результат – нуль або денормалізоване число.
- Inexact (не точно) – потребує заокруглення, результат неможливо представити точно. Результат – заокруглення згідно обраного режиму.
В будь якому випадку, результат за замовчуванням обрано так, щоб він, у більшості випадків, давав бажаний (типовому користувачу) результат операції.
Механізми для їх обробки можуть бути різними:
- власне, апаратні виключення, за виконання під керуванням операційної системи – ймовірно, спершу опрацьовані нею і передані прикладній програмі тим чи іншим способом,
- встановлені певні прапорці у відповідних регістрах.
Далі є кілька прикладів.
Апаратна реалізація IEEE 754
Не намагаючись бути вичерпним, можна навести такі приклади:
- FP16 підтримується ARM, в тому числі – додатковий варіант, без NaN і безмежності. Також, AVX-512-FP16 розширення x86; розширення Zfh та Zfhmin RISC-V, розширення VSX Power ISA.
- Використовується в комп’ютерній графіці та AI.
- FP32 i FP64 – базові типи, які підтримуються багато де, важче знайти, де не підтримуються.
- FP128 підтримується багатьма ISA – IBM System/390 G5, SPARC V8 і V9, Q-розширення RISC-V тощо.
- FP256 – поки не знайшов жодного прикладу.
- FP80 підтримується FPU сімейства x87.
- Зараз цей формат вважається застарілим і не рекомендованим до використання. Однак, див. на вікіпедії аргументи за цей тип.
Little endian та big endian
Не заглиблюючись тут в подробиці – це тема іншої глави, нагадаємо, що x86, RISC-V та більшість ARM – Little endian, тому в пам’яті порядок байтів буде зворотним – про це важливо пам’ятати, аналізуючи дампи пам’яті із floating point-числами.
IEEE 754 в програмуванні
Підтримка мовами програмування
Найбільш широко використовуваними типами є FP64 та FP32. Власне, якщо немає особливих вимог, розумним вибором є FP64.
- В С та С++, зазвичай15, double є FP64, а float – FP32.
- Важливий виняток – для AVR8, MCU із Arduino, використовується і double i float – FP32.
- В Python тип float – це double з C/C++.
- Rust їх так і називає f64 та f32.
- Lua до версії 5.0 включно використовувала double як єдиний числовий тип
number. В новіших таки виділили окремий цілий тип.- Навіть в Lua 5.0 це можна було змінити під час компіляції інтерпретатора.
- Lua покладається на те, що арифметика з цілими числами, збереженими як floating point, залишається точною – без похибки заокруглення, для будь-яких цілих чисел, які можна зберегти точно.
- FORTRAN: real64 та real32.
- Java поводить себе схоже на типовий варіант С++ – double 64-бітовий, float 32-бітовий.
- FP16: Підтримується багатьма бібліотеками, типу OpenGL, Direct3D та D3DX, Vulkan та багатьма бібліотеками нейронних мереж.
- GCC реалізовує тип
__fp16чи_Float16на ARM i x86 з SSE2 відповідно, подробиці див. “Half-Precision Floating Point”. - Clang підтримує
__fp16на всіх платформах,_Float16і__bf16на окремих, детальніше див. Half-Precision Floating Point. - CUDA називає
__half. - В MSVC: в DirectXMath є HALF.
- С++23 додав std::float16_t.
- GCC реалізовує тип
- FP128:
- AArch64 ABI, Application Binary Interface – для 64-бітових ARM, вимагає, щоб тип long double був FP128.
- GCC реалізовує long double як FP128 на PowerPC і SPARC (але з нюансами) та нестандартний тип __float128 на деяких платформах. Новіший Fortran – real(real128), або як нестандартне, але поширене розширення: REAL*16. C++23 додав std::float128_t.
- FP256: реалізацій в компіляторах та апаратному забезпеченні не знайшов16. Однак, за потреби, є великий список бібліотек, які реалізовують схожі засоби:
- GMP – GNU Multiple Precision Arithmetic Library – цілі типи, раціональні чиста та числа з рухомою крапкою довільної точності. Дуже ретельно тестована. Може відхилятися від IEEE-754.
- GNU MPFR Library – бібліотека чисел із рухомою крапкою довільної довжини, реалізована на основі GMP, але дотримується вимог IEEE-754 щодо заокруглення, тому результати мають бути відтворювані на комп’ютернах різних архітектур.
- GNU MPC – реалізація узагальнення IEEE-754 на комплексні числа довільної точності, базується на MPFR.
- List of arbitrary-precision arithmetic software – список таких бібліотек, але різної яксті і різного підходу до акуратності.
- FP80 з x87: long double GCC та Clang для x86, за замовчуванням, використовують цей тип, також надають тип __float80. Ремарка: MSVC не підтримує доступу до цієї можливості x87, не підтримують цей тип.
Інформація про типи C/C++
Через невизначеність типів, таких як double, в стандартах на відповідні мови, С та С++ надають інструменти отримати – а який же той double є на конкретній системі.
Для С++ це шаблон std::numeric_limits, який для floating point типів: float, double, long double, поміж іншого, визначає такі статичні константи:
std::numeric_limits<T>::is_exact== false,- has_infinity17 == true,
- has_quiet_NaN,
- has_signaling_NaN,
- has_denorm (визнано застарілим в C++2318),
- has_denorm_loss (визнано застарілим в C++23),
- round_style, значення з std::float_round_style,
- is_iec559 – є числом, що описується стандартом IEEE 754 / IEC 55919,
- digits – кількість, фактично, двійкових, цифр,
- digits10 – кількість десяткових цифр, (6, 15, 18 для binary32, 64 i 80 відповідно),
- max_digits10,
- min_exponent,
- min_exponent10,
- max_exponent,
- max_exponent10,
- tinyness_before.
та такі статичні функції20:
- min() – для floating point, мінімальне нормалізоване число,
- lowest() – мінімальне денормалізоване число,
- max(),
- epsilon() – віддаль від 1 до наступного числа, яке можна представити,
- round_error() – максимальна похибка заокруглення до цілого, 0.5,
- infinity() – значення безмежності для типу,
- quiet_NaN() – повертає відповідний qNaN,
- signaling_NaN().
С для цього ж використовує макроси, по три – для кожного типу: FLT_DECIMAL_DIG, DBL_DECIMAL_DIG, LDBL_DECIMAL_DIG; FLT_MIN, DBL_MIN, LDBL_MIN тощо, див. C numeric limits interface.
Програмне керування для x86/x87 – низькорівневе
Розглянемо деякі аспекти керування обчисленнями з рухомою крапкою. Розпочнемо з x86.
Керування виключеннями в x86
Сучасний x86 містить два види обчислювачів для виконання операцій над числами з рухомою комою – SIMD розширення SSE21 та x8722 FPU.
Ремарка: x87 FPU вважається legacy – залишком ‘‘темних віків’’, який присутній для зворотної сумісності, але який не бажано використовувати. Однак, на практиці він все ще іноді використовується23, тому, в загальному випадку, ви не знаєте – чи скористався ваш компілятор ним, якщо ви це не заборонили явно, відповідними опціями.
Керування роботою SSE здійснюється за допомогою регістра MXCSR, FPU – за допомогою регістра контролю, а побачити його стан можна за допомогою регістра статусу.
Біти MXCSR (SSE) від 7 до 12 маскують (заборонять, коли встановлені в 1) відповідні floating point виключення. Альтернативно довідатися про такі ситуації можна за допомогою бітів від 0 до 5 цього регістра – втрата точності (UE), ZE – ділення на нуль, чи DF – прапорець денормалізованого числа.
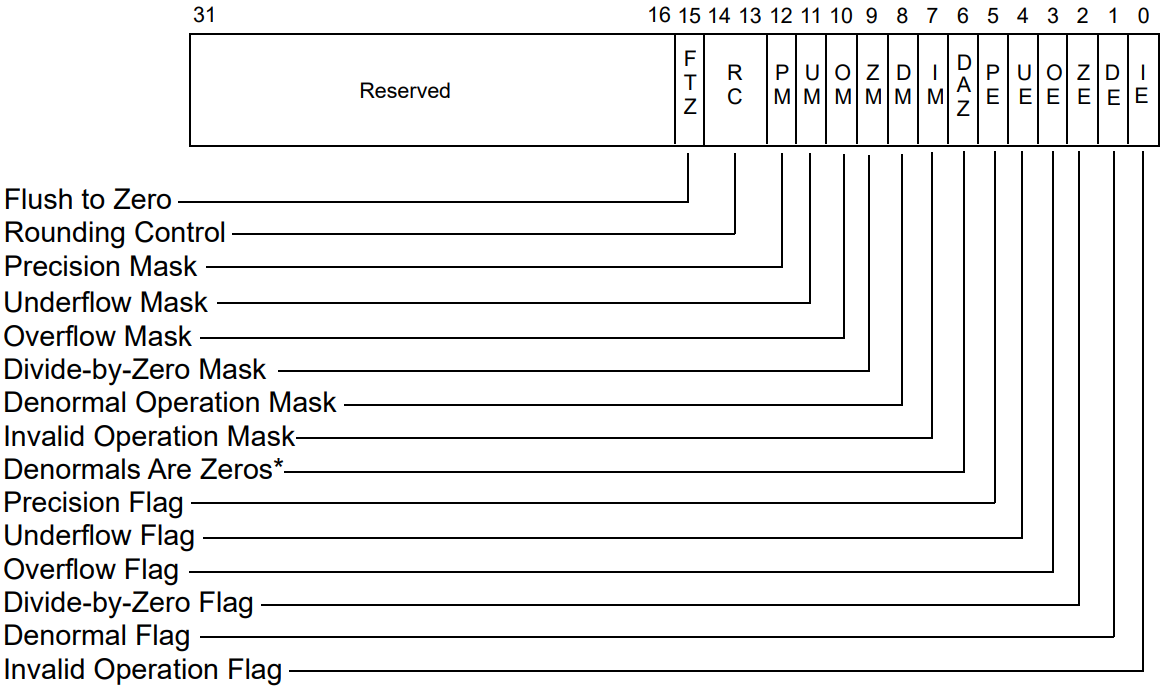 |
|---|
| Регістр керування та статусу SSE, MXCSR. Зображення з “Intel 64 and IA-32 Architectures Software Developer’s Manual, Combined Volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D, and 4”. |
Аналогічні функції виконують біти 0-5 регістрів контролю та статусу x87 FPU.
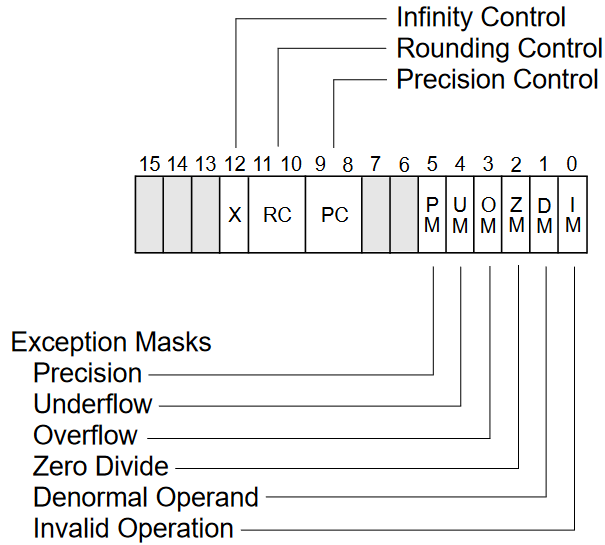 |
|---|
| Контрольний регістр x87 FPU. Зображення з “Intel 64 and IA-32 Architectures Software Developer’s Manual, Combined Volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D, and 4.” |
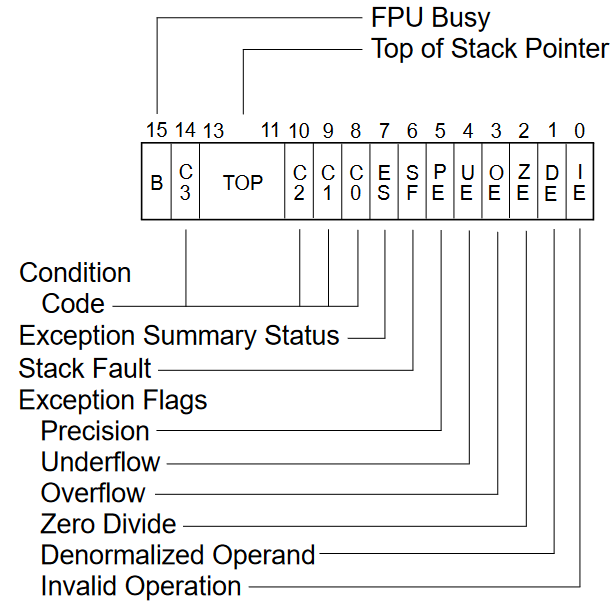 |
|---|
| Регістр статусу x87 FPU. Зображення з “[Intel 64 and IA-32 Architectures Software Developer’s Manual, Combined Volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D, and 4].(https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html)” |
Із цими виключеннями пов’язані відповідні апаратні виключення – int 0x10 (FPU) та int 0x13 (SSE), але, оскільки вони заховані від нас операційною системою, ми їх не розглядатимемо.
На inline-асемблері GCC керувати регістрами x87 можна якось так, де fnstcw – мнемоніка для читання значення з контрольного регістру, а fldcw – для запису в нього:
unsigned int cw;
__asm__ __volatile__ ("fnstcw %0" : "=m" (*&cw));
// Встановлюємо IM, ZM, OM:
cw &= ~(0x01 | 0x04 | 0x08);
__asm__ __volatile__ ("fldcw %0" : : "m" (*&cw));
Також, GNU C Library – glibc, включає інтринсики для керування FPU x87, оголошені в файлі заголовків fpu_control.h, з макросами _FPU_GETCW та _FPU_SETCW, які відповідають асемблерним вставкам вище та набором констант для різних прапорців та режимів роботи FPU:
#include <fpu_control.h>
// Заокругляти до найближчого, внутрішня точність -- 64 біти,
// переривання від FPU заборонені.
fpu_control_t cw;
_FPU_GETCW(cw);
cw |= _FPU_RC_NEAREST | _FPU_DOUBLE;
_FPU_SETCW( cw );
....................
// Повертаємо налаштування за замовчуванням:
cw = _FPU_DEFAULT;
_FPU_SETCW( cw );
Приклад керування регістрами SSE без використання асемблера, див. далі.
Керування заокругленням для x86
Регістри, розглянуті вище, містять біти керування заокругленням.
Для MXCSR це біти 13 та 14 – підтримуються всі комбінації із стандарту, окрім заокруглення від нуля:
- 00b – заокругляти до найближчого (парного),
- 01b – до мінус безмежності,
- 10b – до плюс безмежності,
- 11b – до нуля.
Для x87 FPU – це біти 10-11 контрольного регістру, їх формат відповідає формату бітів 13-14 MXCSR.
Додаткова точність 80-бітового представлення
Також, біти 10-11 контрольного регістру FPU x87 дозволяють керувати точністю внутрішнього представлення – з використанням бітів мантиси 32-бітового, 64-бітового чи 80-бітового представлення.
Іноді використання 80-бітового внутрішнього представлення може спричиняти загадкові проблеми – гайзенбаґ, який зникає від спроб, наприклад, вивести проміжний результат. Причина – різниця між результатом, коли всі дані залишалися в регістрах FPU і коли компілятор вирішив їх зберегти в оперативну пам’ять як 64-бітовий тип, втративши при цьому частину бітів. Проблема тут не в точності чи її втраті, а в виникненні розбіжності. Приклад: “How I joined the bug 323 community”.
Вимкнення денормалізованих чисел для SSE (x86)
GPU, SIMD-розширення та DSP-розширення часто або не підтримують денормалізовані числа взагалі, або дозволяють вимикати їх.
SIMD розширення SSE від Intel x86 містить два пов’язаних біти у регістрі MXCSR – біт 15, Flush-To-Zero (FTZ) та біт 6, Denormals-Are-Zeros (DAZ), див. відповідний рисунок. Перший змушує процесор (якщо виключення заборонені), заокругляти денормалізовані результати до нуля, другий – виконувати це і перед операцією.
Стандартного способу керування немає, але за допомогою інтринсик можна зробити якось так:
#include <xmmintrin.h>
....................
_mm_setcsr(_mm_getcsr() | 0x0040); // Set DAZ
_mm_setcsr(_mm_getcsr() | 0x8000); // Set FTZ
_mm_setcsr(_mm_getcsr() & ~0x8040); // Clear both
Також, можуть бути доступними такі макроси:
#include <pmmintrin.h>
_MM_SET_DENORMALS_ZERO_MODE(_MM_DENORMALS_ZERO_ON);
#include <xmmintrin.h>
_MM_SET_FLUSH_ZERO_MODE(_MM_FLUSH_ZERO_ON);
ARM AArch64
Між 32-бітним (AArch32) та 64-бітним (AArch64) варіантами ARM є певні нетривіальні відмінності. Також, зворотна сумісність AArc64 – підтримка 32-бітного коду, робить опис регістрів цієї ISA дещо плутаним. Заради лаконічності не будемо заглиблюватися в окремий розгляд 32-бітного варіанту.
Ця ISA має 32 128-бітних регістри для floating point та SIMD: v0-v32. Однак, хай число 128 не вводить в оману – ні ARMv8, ні ARMv9 не мають операцій над 128-бітними числами з рухомою крапкою. Їх “нижні” частини доступні як D0-D31, S0-S31, H0-H31 із очікуваним розміром.
Іронічно, що хоча ABI вимагає 128-бітного long double, підтримка його програмна, і місцями – нетривіальна у використанні.
Для керування floating point використовується регістр Floating Point Control Register – FPCR. Він 64-бітний, але використовуються тільки молодші 32 біти.
В AArch32 аналогічний регістр називається FPSCR. Зворотна сумісність AArc64 робить опис регістрів цієї ISA дещо плутаним, заради лаконічності не буду заглиблюватися.
 |
|---|
| ARM AArch64 FPCR. RES0 – зарезервовано, має бути 0. |
Там багато цікавих бітів, автору суб’єктивно видається, що більше, ніж в інших розглянутих ISA:
- AHP – використовувати стандартний (IEEE 754) чи альтернативний формат FP16 під час операцій.
- DN – пропагувати NaN-и чи використовувати NaN за замовчуванням24.
- FZ – “Flushing denormalized numbers to zero”,
- AH – визначає, відбувається це і при вводі (input) і при виводі (output), чи лише при виводі
- FIZ – це ж для читання (input),
- FZ16 – те ж для 16-бітних типів.
- RMode – режим заокруглення: до найближчого, до + чи - безмежності, до нуля.
- IDE, IXE, UFE, DZE, IOE – чи встановлювати відповідні біти із FPSR, якщо сталися певні floating point виключення.
Доступ до цього регістра за допомогою асемблера:
MRS X1, FPCR
MSR FPCR, X1
Статус частково доступний у регістрі Floating Point Status Register – FPSR25. Він, в основному, має справу із виключними ситуаціями SIMD, такими як втрата точності чи насичення.
Результати порівняння floating point чисел зберігаються в цілочисельних прапорцях PSTATE.NZCV – Negative-Zero-Carry-oVerflow.
PSTATE автора цього тексту дещо дивує. Його не називають регістром прапорців, хоча всім його нагадує. Також, видається, немає команди звертатися безпосереднього до нього – хіба до його частин, таких як NZCV. Здійснюється це командами MRS (“Move from system register”) та MSR (“Move to processor state field” / “Move to system register”). Але під час виключень він весь зберігається в Saved Program Status Register.
MRS x1, NZCV
MSR NZCV, x1
Ремарка: аналог FPCR та FPSR для AArch32 – FPSCR, Floating Point-Status and Control Register. Аналог PSTATE – Current Program Status Register, CPSR, який теж вважається системним регістром, і потребує MRS/MSR для доступу.
RISC-V
ISA RISC-V зроблена зручною для розширення. Такі речі, як підтримка floating point є стандартизованими розширеннями. Базові26 floating-point розширення, які додають блок floatin point регістрів, такі:
- F – Standard Extension for Single-Precision Floating-Point,
- D – Standard Extension for Double-Precision Floating-Point,
- Q – Standard Extension for Quad-Precision Floating-Point,
- Zfh – Half-Precision Floating-Point.
А також – цілий блок floating point обчислень в цілочисельних регістрах, які містять всі релевантні команди із попередніх розширень, але, через використання цілочисельних регістрів, несумісні з попередніми:
- Zfhmin – Minimal Half-Precision Floating-Point (лише завантаження-вивантаження-перетворення),
- Zfinx – Single-Precision Floating-Point in Integer,
- Zdinx – Double-Precision Floating-Point in Integer,
- Zhinx – Half-Precision Floating-Point in Integer Register,
- Zhinxmin – Minimal Half-Precision Floating-Point in Integer Register.
Ремарка: через обмежений досвід роботи з RISC-V, можу спотворювати нюанси – буду вдячний за відгуки.
Для керування поведінкою цих розширень використовується регістр fcsr – Floating-Point Control and Status Register.
 |
|---|
| RISC-V fcsr, взято тут. |
Цікаво, що є (псевдо)команди27 доступу до цілого регістру (FRCSR та FSCSR), але, також – до його частин, скажімо – до режиму заокруглення (FRRM та FSRM).
Команди роботи з числами з рухомою крапкою можуть мати або закодований в опкоді режим заокруглення або обирати динамічний, вказаний цим регістром.
Власне, стандарт С, фактично вимагає наявності динамічного режиму.
Виключення, принаймні, базово, не підтримуються – лише встановлюються відповідні прапорці.
Alpha AXP
Alpha AXP ISA, на жаль, закинута, але цікава. Зокрема, вона підтримує як IEEE floating point, так і VAX FP – див. дискусію щодо стандартизації.
Кілька слів про VAX Floating point:
- Ідея та ж, що й за IEEE числами.
- Однак, денормалізованих чисел немає.
- Для ще більш глибокої сумісності, з PDP-11 FP, формат трішки дивний – різні частини переплутані.
- Існує D_floating та G_floating – обидва 64-бітові, але з експонентою різного розміру. Також – H_floating, 128-бітовий тип.
- 64-бітовий D_floating відрізняється від 32-бітового F_floating лише додатковими 32-ма бітами дробової частини – мантиси.
- Від’ємного нуля, NaN чи безмежностей – немає.
- Вважається, що ліворуч є неявна одиничка, перед якою – крапка.
- Тобто, якщо мантиса має вигляд “abc…”, це інтерпретується як “0.1abc…” – значення мантиси чисел знаходяться між 0.5 і 1 – на відміну від нормалізованих IEEE чисел, які між 1 і 2.
 |
|---|
| Приклад F_floating числа – VAX FP. Зауважте, що дробова частина не неперервна, розбита на дві. Її можна просто відкинути, із втратою точності, звичайно. Bias = 128, не 127 як для IEEE 754 FP32. Таблицю взято тут. |
GCC, теоретично, вміє їх використовувати – див. опцію -mfloat-vax.
Детальніше поки не розглядаємо, але див. Alpha AXP Architecture Reference Manual, стор. 4-68, Floating-Point Control Register (FPCR).
SPARC v9
ISA SPARC все ще розвивається Oracle. Обмежуся посиланням на v9, оскільки відповідна апаратура є в нас – Sun fire v890, на UltraSparc IV+.
Із цікавих особливостей – можливість використовувати два 64-бітних floating point регістри як один 128-бітний.
Підхід до керування – менш-більш стандартний, див. Weaver, D. L.; Germond, T., eds. (1994). The SPARC Architecture Manual, Version 9, “5.1.7 Floating-Point State Register (FSR)”, на стор. 62.
CUDA
Починаючи з Compute capability (CC) 2.0, підтримується стандарт IEEE 754. Існує також швидкий режим для FP32, який вмикається ключем компілятора -ftz=true – денормалізовані числа заокругляються до нуля, також ключі -prec-div=false та -prec-sqrt=false дозволяють обчислювати ділення та отримання квадратного кореня із точністю, що гірша за останній біт, але швидше.
Невелика відмінність в точності може бути для складніших функцій, зокрема, тригонометричних.
Режими заокруглення вказуються у кожній команді окремо. Аналога регістра стану чи виключень немає.
Детальніше див. CUDA and Floating Point.
Програмне керування – високорівневе
Стандартні засоби C та C++
Навіть на прикладі x86 бачимо проблему – в межах одного процесора присутні різні способи керування заокругеленням, виключеннями та деякими іншими аспектами роботи із floating point-типами. У інших процесорів ці способи будуть помітно відрізнятися, хоча, зазвичай, все ж, зводитимуться до маніпуляцій певних бітів певних регістрів. Також, відрізнятимуться між реалізаціями і нюанси навіть в межах однієї ISA.
Ускладною ситуацію те, що ABI конкретних платформ (CPU + ОС + компілятор) – їх бінарний інтерфейс, накладає обмеження на режими обчислень з рухомою крапкою. Змінюючи його в певній функції, завжди потрібно відновлювати, перш ніж переходити до коду, який може очікувати стандартного, для цього ABI, режиму.
Стандарти C99 та С++11 надали, до певної межі, уніфіковані засоби керування цією конфігурацію – як вони називають, ‘‘Floating-point environment’’.
Ці засоби оголошено в файлах заголовків
Формально, вважається, що інструменти, перераховані далі, працюють лише за використання директиви:
#pragma STDC FENV_ACCESS ON
Без неї, в теорії, реалізація вважатиме, що всі налаштування – за замовчуванням. На практиці, більшість компіляторів дозволяють модифікацію середовища і без неї. Компілятор Visual Studio цієї директиви не знає, але має аналог:
#pragma fenv_access (on)
Щоправда, цей аналог більш інтрузивний, забороняє оптимізації обчислень з рухомою крапкою, тому може ламати обчислення floating point виразів під час компіляції тощо.
Тип std::fenv_t описує floating point середовище.
Пара функцій дозволяє його прочитати у змінну із відповідного апаратного забезпечення (наприклад, розглянутих раніше регістрів), або записати у апаратне середовище:
int fegetenv( std::fenv_t* envp );
int fesetenv( const std::fenv_t* envp );
Поміж іншого, цим функціям можна передати консанту FE_DFL_ENV, яка переведе середовище у стан за замовчуванням.
Керування заокругленням
Наступна пара функцій керує напрямком заокруглення:
int fesetround( int round ); // Встановити
int fegetround(); // Прочитати
де заокруглення визначаються одним із наступних макросів: FE_DOWNWARD, FE_UPWARD, FE_TONEAREST, FE_TOWARDZERO. Реалізації можуть мати додаткові режими, але макроси оголошуються лише, якщо відповідний режим підтримується.
Обчислення під час компіляції завжди відбуваються в режимі
FE_TONEAREST. Цей режим часто є за замовчуванням і під час виконання.
Зауважте, що FE_UPWARD означає, наприклад, що 1.00000000001 буде заокруглено до 2.
Додатково, взнати поточний режим заокругелення можна за допомогою макросу FLT_ROUNDS з <cfloat>, можливі константи якого відповідають значенням std::float_round_style. Як відбувається заокруглення за замовчуванням, під час перетворення у різні типи, див. [std::numeric_limits
Також, С++ має цілий зоопарк функцій заокруглення.
- std::rint() і сімейство28 – заокруглення, з використанням поточного режиму заокруглення.
- std::nearbyint() – те ж, хіба ніколи не спричиняє виключну ситуацію FE_INEXACT.
- Обидві ці функції, коли режим заокруглення FE_TONEAREST,
X.5заокруглюють до до парного.
- Обидві ці функції, коли режим заокруглення FE_TONEAREST,
- std::round() – заокруглює до найближчого, ігноруючи режим заокруглення,
X.5заокруглює від нуля (до безмежності того ж знаку), на відміну від rint() та nearbyint(). - std::floor() – заокругляє вниз, до меншого. Для додатних – еквівалентно відкиданню дробової частини, але це невірно для від’ємних.
- std::ceil() – заокругляє вверх, до більшого. Для від’ємних – еквівалентно відкиданню дробової частини
- std::trunc() – відкидає дробову частину. Еквівалентне заокругленню до нуля.
Заокруглення до вказаної кількості десяткових цифр, на жаль, в стандартній бібілотеці немає. Можна скористатися таким трюком:
std::rint( x * 10)/10, але щодо суворої відповідності вимогам заокруглення IEEE 754, можуть бути нюанси.Зокрема, в рамках “The One Billion Row Challenge”, потрібно виводити одну десяткову цифру після крапки, з заокруленням до безмежності. Єдиний варіант, який вдалося змусити працювати:
std::round(val.mean/val.quantity*10.0 + 0.5)/10.0, не зважаючи на режими заокруглення. Зокрема, невірне заокруглення давалиstd::fesetround(FE_UPWARD); std::rint(val.mean/val.quantity*10.0)/10.0;. Ймовірно, щось роблю не так…
Приклад функціонування різних заокруглень. Виконано для GCC 11.4 з опцією -frounding-math, яка вимагає суворого дотримання правил заокруглення IEEE 754. Також, показано (стовпчики N.S. – non-strict), де результати для цього компілятора, за ввімкненої оптимізації, відрізняються.
| Дія | TONEAREST | TOWARDZERO | DOWNWARD | N.S. | UPWARD | N.S. |
|---|---|---|---|---|---|---|
| rint(1.00000000001) | 1 | 1 | 1 | 2 | ||
| rint(1.4) | 1 | 1 | 1 | 2 | ||
| rint(1.5) | 2 | 1 | 1 | 2 | ||
| rint(1.6) | 2 | 1 | 1 | 2 | ||
| rint(2.5) | 2 | 2 | 2 | 3 | ||
| rint(-1.00000000001) | -1 | -1 | -1 | -1 | -1 | -2 |
| rint(-1.6) | -2 | -1 | -1 | -1 | -1 | -2 |
| rint(-1.4) | -1 | -1 | -1 | -1 | -1 | -2 |
| rint(-1.5) | -2 | -1 | -1 | -1 | -1 | -2 |
| rint(-2.5) | -2 | -2 | -2 | -2 | -2 | -3 |
| nearbyint(1.00000000001) | 1 | 1 | 1 | 2 | ||
| nearbyint(1.4) | 1 | 1 | 1 | 2 | ||
| nearbyint(1.5) | 2 | 1 | 1 | 2 | ||
| nearbyint(1.6) | 2 | 1 | 1 | 2 | ||
| nearbyint(2.5) | 2 | 2 | 2 | 3 | ||
| nearbyint(-1.00000000001) | -1 | -1 | -1 | -1 | ||
| nearbyint(-1.6) | -2 | -1 | -1 | -1 | ||
| nearbyint(-1.4) | -1 | -1 | -1 | -1 | ||
| nearbyint(-1.5) | -2 | -1 | -1 | -1 | ||
| nearbyint(-2.5) | -2 | -2 | -2 | -2 | ||
| round(1.00000000001) | 1 | 1 | 1 | 1 | ||
| round(1.4) | 1 | 1 | 1 | 1 | ||
| round(1.5) | 2 | 2 | 2 | 2 | ||
| round(1.6) | 2 | 2 | 2 | 2 | ||
| round(2.5) | 3 | 3 | 3 | 3 | ||
| round(-1.00000000001) | -1 | -1 | -1 | -1 | ||
| round(-1.6) | -2 | -2 | -2 | -2 | ||
| round(-1.4) | -1 | -1 | -1 | -1 | ||
| round(-1.5) | -2 | -2 | -2 | -2 | ||
| round(-2.5) | -3 | -3 | -3 | -3 | ||
| floor(1.00000000001) | 1 | 1 | 1 | 1 | ||
| floor(1.4) | 1 | 1 | 1 | 1 | ||
| floor(1.5) | 1 | 1 | 1 | 1 | ||
| floor(1.6) | 1 | 1 | 1 | 1 | ||
| floor(2.5) | 2 | 2 | 2 | 2 | ||
| floor(-1.00000000001) | -2 | -2 | -2 | -2 | ||
| floor(-1.6) | -2 | -2 | -2 | -2 | ||
| floor(-1.4) | -2 | -2 | -2 | -2 | ||
| floor(-1.5) | -2 | -2 | -2 | -2 | ||
| floor(-2.5) | -3 | -3 | -3 | -3 | ||
| ceil(1.00000000001) | 2 | 2 | 2 | 2 | ||
| ceil(1.4) | 2 | 2 | 2 | 2 | ||
| ceil(1.5) | 2 | 2 | 2 | 2 | ||
| ceil(1.6) | 2 | 2 | 2 | 2 | ||
| ceil(2.5) | 3 | 3 | 3 | 3 | ||
| ceil(-1.00000000001) | -1 | -1 | -1 | -1 | ||
| ceil(-1.6) | -1 | -1 | -1 | -1 | ||
| ceil(-1.4) | -1 | -1 | -1 | -1 | ||
| ceil(-1.5) | -1 | -1 | -1 | -1 | ||
| ceil(-2.5) | -2 | -2 | -2 | -2 | ||
| trunc(1.00000000001) | 1 | 1 | 1 | 1 | ||
| trunc(1.4) | 1 | 1 | 1 | 1 | ||
| trunc(1.5) | 1 | 1 | 1 | 1 | ||
| trunc(1.6) | 1 | 1 | 1 | 1 | ||
| trunc(2.5) | 2 | 2 | 2 | 2 | ||
| trunc(-1.00000000001) | -1 | -1 | -1 | -1 | ||
| trunc(-1.6) | -1 | -1 | -1 | -1 | ||
| trunc(-1.4) | -1 | -1 | -1 | -1 | ||
| trunc(-1.5) | -1 | -1 | -1 | -1 | ||
| trunc(-2.5) | -2 | -2 | -2 | -2 |
Інше
Більше подробиць – а їх трохи є(!), можна побачити за посиланням: “Floating-point environment29”. Зокрема, там описано керування виключеннями – наведу приклад звідти:
#include <cfenv>
#include <cmath>
#include <iostream>
// #pragma STDC FENV_ACCESS ON
volatile double zero = 0.0; // volatile not needed where FENV_ACCESS is supported
volatile double one = 1.0; // volatile not needed where FENV_ACCESS is supported
int main()
{
std::feclearexcept(FE_ALL_EXCEPT);
std::cout << "1.0/0.0 = " << 1.0 / zero << '\n';
if (std::fetestexcept(FE_DIVBYZERO))
std::cout << "division by zero reported\n";
else
std::cout << "division by zero not reported\n";
std::feclearexcept(FE_ALL_EXCEPT);
std::cout << "1.0/10 = " << one / 10 << '\n';
if (std::fetestexcept(FE_INEXACT))
std::cout << "inexact result reported\n";
else
std::cout << "inexact result not reported\n";
std::feclearexcept(FE_ALL_EXCEPT);
std::cout << "sqrt(-1) = " << std::sqrt(-1) << '\n';
if (std::fetestexcept(FE_INVALID))
std::cout << "invalid result reported\n";
else
std::cout << "invalid result not reported\n";
}
POSIX
Стандарт POSIX включає засоби, пов’язані із floating point, які, в цілому, співпадають із прийнятими в стандарти C та C++. Додатково вартує згадати сигнал SIGFPE – Signal on Floating Point Error. Це програмний інтерфейс до виключень IEEE 754 в прикладному коді.
Нестандартні засоби – MSVC
Компілятор MS Visual Studio надає свої засоби для керування середовища floating point:
- _controlfp_s() – прочитати чи змінити контрольний регістр. Кросплатформова. За посиланням є згадки і більш спеціалізованих функцій – _control87(), _controlfp(), __control87_2() та _status87, _statusfp, _statusfp2.
- _clearfp() – очистити всі виключення, кросплатформовий варіант. Її спеціалізований варіант – _clear87().
Приклади з офіційної документації:
unsigned int current_word = 0;
_controlfp_s(¤t_word, _DN_SAVE, _MCW_DN);
// Denormal values preserved on ARM platforms and on x64 processors with
// SSE2 support. NOP on x86 platforms.
_controlfp_s(¤t_word, _DN_FLUSH, _MCW_DN);
// Denormal values flushed to zero by hardware on ARM platforms
// and x64 processors with SSE2 support. Ignored on other x86 platforms.
Інтерфейсом до виключень можуть бути структуровані виключення MSVC. Детальніше ми їх поки не розглядатимемо.
Звичайно, новіші версії цього компілятора підтримують також стандартні засоби.
GCC -ffast-math
Стандарт IEEE 754 розроблений так, щоб забезпечувати відтворюваність результатів на різних платформах та можливість аналізу комп’ютерних чисельних обчислень і отримання гарантій точності. Це важливо для багатьох критичних розрахунків. Однак, суворе дотримання вимога стандарту дуже обмежує оптимізації, які може застосувати компілятор і, як наслідок, може призводити до величезного сповільнення.
Оскільки така строгість потрібна далеко не завжди, багато компіляторів підтримують більш “розслаблений” режим, який дозволяє виконувати код швидше.
Для компілятора GCC він вмикається опцією -ffast-math. Він відповідає наступним прапорцям:
-funsafe-math-optimizations– може змінювати контрольні регістри під час запуску програми, включає:-fno-signed-zeros– ігнорує знак нуля, дозволяє оптимізувати операції виду 0.0*x чи 0.0+x.-fno-trapping-math– компілює код, вважаючи, що не буде відбуватися floating point виключень,-fassociative-math– дозволяє переставляти операції, може трохи змінювати результат, зокрема – знак нуля, відкриваючи безліч оптимізацій та використання SIMD, але й може зламати деякі акуратні підходи до збільшення точності обчислень з рухомою крапкою, наприклад, Алгоритм Кехена (Kahan summation),-freciprocal-math– дозволяє заміняти x/y на x*(1/y), оскільки, на багатьох платформах, 1/y можна обчислити швидше, ніж ділення, а також дозволяє мінімізувати кількість доволі затратних ділень – якщо кілька чисел потрібно поділити на певну величину, з цим прапорцем, компілятор може обчислити її обернене значення та множити на нього.- Сам по собі цей прапорець дозволяє матиматичні оптимізації, виду
sqrt(x) * sqrt(x) = x,exp(x) * exp(y) = exp(x+y)тощо.
-ffinite-math-only– компілює, вважаючи, що аргументи та результати операцій не будуть безмежностями чи NaN, без цього навіть значення виразуx-xне дорівнює 0.0, з точки зору компілятора,-fno-math-errno– не встановлювати errno у математичних функціях типу sqrt, це може сильно прискорити програму, особливо в багатопоточному середовищі та не порушує сумісності із IEEE 754, (щоправда, функції типу malloc чи strdup теж можуть перестати змінювати errno),-fno-signaling-nans– вважає, що не буде виключень, спричинених NaN,-fno-rounding-math– вважаємо, що заокруглення до найближчого,-fcx-limited-range– оптимізує ділення та множення комплексних чисел,-fexcess-precision=fast– на різних системах можуть бути типи, які дають більшу точність, ніж вимагає IEEE 754, наприклад 80-бітний long double x87, цей прапорець дозволяє використовувати такий режим, якщо він дозволяє створити швидший код.
Також, створюється макрос __FAST_MATH__ для виявлення використання цієї опції в коді.
З іншого боку, за замовчуванням, GCC використовує заокруглення до найближчого і не повідомляє навіть про signaling NaN. Ефект від цього можна побачити у табличці вище. Більш строгої відповідності стандарту можна досягнути опціями -frounding-math та ‘‘-fsignaling-nans’’.
Детальніше див. Optimizations enabled by -ffast-math, Semantics of Floating Point Math in GCC та Options That Control Optimization.
Також, GCC підтримує ввімкнення цього режиму лише для окремих функцій (інший спосіб):
__attribute__((optimize("-ffast-math")))
double mul2(double val) {
return val / 2;
}
#pragma GCC optimize("-ffast-math")
double mul2(double val) {
return val / 2;
}
Застереження щодо використання цієї опції: ‘‘Beware of fast-math’’.
Ремарка. Дуже хороша обчислювальна бібліотека, GSL – GNU Scientific Library, використовує тести, які чутливі до суворого дотримання стандарту IEEE 754 – заради можливості використовувати її і в чутливих до точності та гарантій обчислень. Успішне проходження цих тестів потребує вимагати від компілятора суворо дотримуватися вимог стандарту. Її засоби керування floating point середовищем: “Setting up your IEEE environment”.
Clang -ffast-math
Аналогічний ключ є і в Clang. Те ж стосується більш суворої відповідності стандарту. Подробиці відрізняються, але, в цілому, його функція та ж. А подробиці – див. у документації.
MSVC – /fp:fast аналог, -ffast-math
Приблизно такі ж оптимізації дозволяє компілятору від Мікрософт ключ /fp:fast. І навпаки, /fp:strict вимагає суворого дотримання стандарту.
Детальніше – див. документацію: /fp (Specify floating-point behavior).
MSVC взагалі має трохи нюансів. Наприклад, цитата з документації на printf-подібні функції: “Starting in Windows 10 version 2004 (build 19041), the printf family of functions prints exactly representable floating point numbers according to the IEEE 754 rules for rounding. In previous versions of Windows, exactly representable floating point numbers ending in ‘5’ would always round up.”
Засоби GSL – GNU Scientific Library
Стандарти C та C++ отримали засоби керування floating point середовищем доволі пізно. Тому, різноманітні бібліотеки мусили шукати свої рішення. Зокрема, вже згадувана вище GSL, тести якої чутливі до суворої відповідності реалізації стандарту IEEE 754, використовує дещо екзотичний, але, певне – зі своїми плюсами, метод.
Функція gsl_ieee_env_setup() встановлює конфігурацію обчислень з рухомою крапкою згідно вмісту змінної середовища GSL_IEEE_MODE. Ця змінна, через кому, вказує потрібну конфігурацію: GSL_IEEE_MODE="double-precision, mask-underflow, mask-denormalized".
Бібліотека дуже хороша! Детальніше розповідати про неї віднесе нас занадто далеко, та й документація в неї гарна – немає потреби дублювати. Тому, враховуючи тему цього тексту, згадаю лише один допоміжний засіб:
int gsl_fcmp(double x, double y, double epsilon);
| Ця функція перевіряє, чи x та y рівні в межах відносної похибки epsilon. Інтервал обирає як: [ | x - y | < 2^k \cdot \mathrm {epsilon}, ] де k – більша з експонент x та y. |
Подробиці див. документацію: “IEEE floating-point arithmetic” та “Approximate Comparison of Floating Point Numbers”.
Засоби Boost
'’Бібліотека бібліотек’’ boost містить цілу секцію математичних бібліотек30. Відзначу поміж них Multiprecision – цілі та з рухомою крапкою числа довільної точності; Rational – динамічні раціональні числа (на противагу статичним, часу компіляції, std::ratio – які теж пішли з однойменної бібліотеки boost); Safe Numerics – безпечні щодо переповнень цілі числа; NumericConversion; але вартує проглянути весь список.
До теми цього тексту безпосереднє відношення має Math Toolkit. Це бібліотека з багатьма засобами, в межах нашої теми цікаві: допомога з float128 типами та “Floating Point Utilities”, зокрема:
- Функції заокруглення та обрізання.
- Порівняння floating point чисел.
- “Sign Manipulation Functions”.
- Послідовний та взаємо-узгоджений ввід-вивід безмежностей та NaN.
- “Floating-Point Representation Distance (ULP), and Finding Adjacent Floating-Point Values”.
- “Condition Numbers” – оцінка чутливості функції до похибок заокруглення.
- “ULPs Plots” – візуалізація точності реалізації floating point функцій.
FP8
Опис
Для тренування розуміння особливостей floating point чисел – чисел з рухомою крапкою, запропоновано вкористовувати крихітний тип FP8, змодельований за IEEE 754, із наступними властивостями:
- 1 біт знаку,
- 4 біти експоненти,
- 3 біти мантиси,
- зсув, bias = 7, \(2^{4-1}-1\),
- зсув для денормалізованих чисел, dn-bias = 6.
Ремарка: це відрізняється від деяких FP8, популярних в Інтернеті. Причин дві – з одного боку, така точність і діапазон видаються кориснішими для потреб курсу, з іншого – дозволяють легко виявляти неуважних чи недобросовісних студентів – хай і найбільш лінивих із них. Зокрема, популярне значення bias = 3. Хоча, за час існування курсу, цей тип вже описано у Вікіпедії, ймовірно, незалежно. Див. також Eight-bit floating point щодо інших форматів.
 |
|---|
| Формат FP8, використований для практичних. |
Розглянемо спеціальні значення цього формату:
| Двійкове представлення | Значення |
|---|---|
| 0 0000 000 | +0.0 |
| 1 0000 000 | -0.0 |
| 0 1111 000 | \(+\infty\) |
| 1 1111 000 | \(-\infty\) |
| x 1111 yyy | NaN |
| x 1111 0yy | Signalling NaN |
| x 1111 1yy | Quiet NaN |
| s 0000 yyy | Денормалізовані числа |
| Решта | Звичайні числа |
Його можна описати наступними характеристиками:
- Максимальне за модулем, не безмежне значення: 240.
- Мінімальне за модулем нормалізоване значення: 0.015625.
- Максимальне за модулем денормалізоване: 0.013671875.
- Мінімальне за модулем, не нульове, денормалізоване значення: 0.001953125.
- Епсилон, віддалі від 1 до наступного, відмінного від 1, числа: 0.125.
Є 242 відмінних значення, вважаючи +0.0 і -0.0 різними.
Таблиця всіх значень:
| s_eeee/mmm | … 000 | … 001 | … 010 | … 011 | … 100 | … 101 | …110 | … 111 |
|---|---|---|---|---|---|---|---|---|
| 0_0000… | 0 | 0.001953125 | 0.00390625 | 0.005859375 | 0.0078125 | 0.009765625 | 0.01171875 | 0.013671875 |
| 0_0001… | 0.015625 | 0.017578125 | 0.01953125 | 0.021484375 | 0.0234375 | 0.025390625 | 0.02734375 | 0.029296875 |
| 0_0010… | 0.03125 | 0.03515625 | 0.0390625 | 0.04296875 | 0.046875 | 0.05078125 | 0.0546875 | 0.05859375 |
| 0_0011… | 0.0625 | 0.0703125 | 0.078125 | 0.0859375 | 0.09375 | 0.1015625 | 0.109375 | 0.1171875 |
| 0_0100… | 0.125 | 0.140625 | 0.15625 | 0.171875 | 0.1875 | 0.203125 | 0.21875 | 0.234375 |
| 0_0101… | 0.25 | 0.28125 | 0.3125 | 0.34375 | 0.375 | 0.40625 | 0.4375 | 0.46875 |
| 0_0110… | 0.5 | 0.5625 | 0.625 | 0.6875 | 0.75 | 0.8125 | 0.875 | 0.9375 |
| 0_0111… | 1 | 1.125 | 1.25 | 1.375 | 1.5 | 1.625 | 1.75 | 1.875 |
| 0_1000… | 2 | 2.25 | 2.5 | 2.75 | 3 | 3.25 | 3.5 | 3.75 |
| 0_1001… | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 |
| 0_1010… | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0_1011… | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| 0_1100… | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 |
| 0_1101… | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 |
| 0_1110… | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 |
| 0_1111… | +Inf | sNaN | sNaN | sNaN | qNaN | qNaN | qNaN | qNaN |
| 1 0000 … | −0 | −0.001953125 | −0.00390625 | −0.005859375 | −0.0078125 | −0.009765625 | −0.01171875 | −0.013671875 |
| 1 0001 … | −0.015625 | −0.017578125 | −0.01953125 | −0.021484375 | −0.0234375 | −0.025390625 | −0.02734375 | −0.029296875 |
| 1 0010 … | −0.03125 | −0.03515625 | −0.0390625 | −0.04296875 | −0.046875 | −0.05078125 | −0.0546875 | −0.05859375 |
| 1 0011 … | −0.0625 | −0.0703125 | −0.078125 | −0.0859375 | −0.09375 | −0.1015625 | −0.109375 | −0.1171875 |
| 1 0100 … | −0.125 | −0.140625 | −0.15625 | −0.171875 | −0.1875 | −0.203125 | −0.21875 | −0.234375 |
| 1 0101 … | −0.25 | −0.28125 | −0.3125 | −0.34375 | −0.375 | −0.40625 | −0.4375 | −0.46875 |
| 1 0110 … | −0.5 | −0.5625 | −0.625 | −0.6875 | −0.75 | −0.8125 | −0.875 | −0.9375 |
| 1 0111 … | −1 | −1.125 | −1.25 | −1.375 | −1.5 | −1.625 | −1.75 | −1.875 |
| 1 1000 … | −2 | −2.25 | −2.5 | −2.75 | −3 | −3.25 | −3.5 | −3.75 |
| 1 1001 … | −4 | −4.5 | −5 | −5.5 | −6 | −6.5 | −7 | −7.5 |
| 1 1010 … | −8 | −9 | −10 | −11 | −12 | −13 | −14 | −15 |
| 1 1011 … | −16 | −18 | −20 | −22 | −24 | −26 | −28 | −30 |
| 1 1100 … | −32 | −36 | −40 | −44 | −48 | −52 | −56 | −60 |
| 1 1101 … | −64 | −72 | −80 | −88 | −96 | −104 | −112 | −120 |
| 1 1110 … | −128 | −144 | −160 | −176 | −192 | −208 | −224 | −240 |
| 1 1111 … | −Inf | sNaN | sNaN | sNaN | qNaN | qNaN | qNaN | qNaN |
Реалістичні FP8
FP8, які використовуються в задачах штучного інтелекту, конструюються по іншому, зокрема, часто, або без безмежностей та NaN, або під них виділено значно меншу кількість біт, ніж в стандарті IEEE 754. Приклад: ‘‘FP8 Formats for Deep Learning’’ згадує два типи:
- 5-бітова експонента та 2-бітова мантиса (E5M2), який відтворює семантику спеціальних значень стандарту. Цей тип залишається сумісним з стандартним FP16 – достатньо відкинути молодший байт, з мантисою.
- 4-бітова експонента та 3-бітова мантиса (E4M3), без безмежностей і з однією комбінацією бітів для NaN.
В обох випадках підтримуються денормалізовані числа.
Вправи
Для більшої ефективності засвоєння, завдання потрібно виконувати наживо, із можливістю використовувати папір та ручку, можливо – простий калькулятор, але не комп’ютер чи Інтернет.
Записати, як десятковий дріб, із поясненням:
- Максимальне за модулем, не безмежне значення.
- Типова помилка – забути про безмежність, і дорахувати до 480.
- Мінімальне за модулем нормалізоване значення.
- Типова помилка – забути про денормалізовані числа і отримати \(2^{-7} = 0.0078125\).
- Максимальне за модулем денормалізоване.
- Мінімальне за модулем, не нульове, денормалізоване значення.
- Епсилон, віддаль від 1 до наступного, відмінного від 1, числа.
Записати спеціальні значення:
- 0.0,
- -0.0, пояснити, звідки він береться,
- \(+\infty\), розповісти, як можна отримати її в обчисленнях,
- \(-\infty\), розповісти, як можна отримати її в обчисленнях,
- NaN, пояснити, що таке корисне навантаження, payload,
- sNaN, пояснити, що це таке і як поводиться,
- qNaN, пояснити, що це таке і як поводиться.
Перетворити із шістнадцяткового представлення у десятковий дріб кілька вказаних чисел. Бажано, щоб поміж них були і спеціальні значення.
Записати десяткові дроби у FP8 представленні. Сказати, чи буде це представлення точним і чому так?
Завдання
Завдання 1
Реалізувати перетворення з бінарного представлення IEEE 754 чисел в текстове і назад:
- FP16,
- FP32 – float в С,
- FP64 – double в С,
- додатково, FP80 – long double для GCC на x86, нестандартний тип, що підтримується x87 FPU.
Потрібно підтримувати денормалізовані числа, Inf і обидва види NaN (signalling та quiet).
Обов’язково реалізувати тестування на достатньо широкому наборі варіантів.
Завдання 2
Реалізувати С++ бібліотеку для роботи із floating point числами заданого розміру – із вказанням кількості біт експоненти та мантиси.
Приклад використання (200 – біт в мантисі, 55 – в експоненті):
my_float<200, 55> v1 = 1.23, v2 = 3.14, v3;
v3 = v1 + v2;
v1 *= v3;
Реалізація повинна бути адекватною з точки зору швидкодії.
Необхідним є представлення в двійковому форматі типу IEEE 754. Зокрема, для 23 біти мантиси та 8 біт експоненти, бінарне представлення повинне відповідати стандартному float, 53/11 – double і т.д.
Потрібно реалізувати всі основні арифметичні операції. Бажаною є підтримка тригонометричних функцій та піднесення до степені (включаючи дробові та від’ємні).
Підтримка користувацьких літералів С++11 бажана, вони, зокрема, спрощують тестування.
Підсумок
- Скічена кількість цифр у представлення floating point чисел спричиняє труднощі, про які потрібно знати та враховувати їх.
- Підхід “машина все степить” тут аж ніяк не працює.
- Зокрема, потрібно пам’ятати про похибку заокруглення та катастрофічне скасування (catastrophic cancellation).
- Не можна порівнювати числа з рухомою крапкою простою операцією ==.
- Однак, робити це правильно – доволі нетривіально і залежить від контексту та задачі.
- Але цілі числа, які вміщаються у представленні, зберігаються точно і операції над ними будуть точними.
- Для запису floating point використовується формат із знаку, експоненти та мантиси.
- Для представлення малих чисел, до експоненти застосовується – віднімається від неї, зсув – bias.
- Біт перед крапкою не зберігається, неявно вважається рівним 1.
- Однак, для кращого представлення малих чисел, якщо експонента нульова, неявно вважається, що перед комою – нуль.
- Такі числа називають денормалізованими (subnormal).
- Їх наявність запобігає втраті точності (underflow), однак, оскільки їх реалізації часто повільніша за нормалізовані числа, іноді цю можливість не додають або вимикають.
- Також, формат передбачає можливість запису спеціальних значень:
- NaN – Not a number, не число, результат некоректних операцій, таких, як квадратний корінь з мінус один.
- \(\pm \infty\) – безмежність, результат ділення на нуль та інших операцій із добре визначеним безмежним результатом.
- Стандарт на floating point – IEEE 754.
- Описує 32-бітний (float в С), 64-бітний (double) та кілька інших форматів.
- Він описує правила заокруглення та можливі виключні ситуації.
- Описує точність арифметичних операцій та бажані складніші математичні функції.
- -ffast-math – важливий ключ GCC, але застосовувати його потрібно акуратно і з розумінням.
Додатки
Fixed point
Альтернативою до floating point – чисел із рухомою крапкою, є числа із фіксованою крапкою – fixed point.
Фізично це “звичайне” ціле число, але програмно вважається, що якась кількість його біт – це дробова частина. Іншими словами, є масштабни фактор – число, на яке потрібно поділити двійкове представлення31, щоб отримати результат, який мається на увазі.
Наприклад, можна взяти звичайний unsigned int, але домовитися, що останні 4 біти – дробова частина. Тоді масштабний фактор – \(2^{4}\).
Тобто, якщо в змінній збережено 01110101b, то за масштабного фактору \(2^{4}\), вважаємо це числом 117d/16d = 7.3125.
Взагалі кажучи, кількість біт дробової частини може бути більшою за кількість біт представлення – че лише означатиме, що можна зберігати лише числа, на відповідну величину менші за 1.
Зазвичай, масштабний фактор буде степінню двійки.
Біт знаку, зазвичай, виділяється явно, а доповнювальний код для від’ємних числе не використовується.
Зараз існує два основних використання такого представлення:
- обчислення на мікроконтролерах із дуже обмеженими ресурсами,
- фінансові обчислення, де чітко задані правила заокруглення копійок, які дещо відрізняються від стандартних правил floating point.
Старіші мови, зокрема PL/I, COBOL, Ada, явно підтримують fixed point – синтаксис у них цікавий, але в сучасних це перекладено на бібліотеки. Див., наприклад, libfixmath – 16.16 арифметика, із трансцендентними функціями, трохи закинута; AVRfix – для AVR8, MCU із Ардуїно, s7.8, s15.16, s7.24, включає транцендентні функції; FPM – C++ header-only, шаблонна, із можливістю вказання кількості біт дробової частини.
В принципі, підтримку раціональних чисел можна вважати узагальненням fixed point.
Детальніше див, наприклад, вікі: Fixed-point arithmetic.
Документ ISO/IEC TR 18037, глава 4 пропонує, поміж інших розширень для мови С, fixed point арифметику. Він частково реалізований, наприклад, в GCC, зокрема – для AVR.
ARM, зокрема ARMv8, AArch64, підтримує fixed-point арифметику, яка включає операції перетворення між fixed point та floating point із вказаною кількістю біт перед двійковою крапкою.
Нестандартні floating point типи
Для спеціалізованих обчислень визначають різні варіації floating-point типів.
Маленькі типи іноді називають minifloats – див. аналіз на вікіпедії. Зокрема, там показано цікаві діаграми для аналізу точності таких типів.
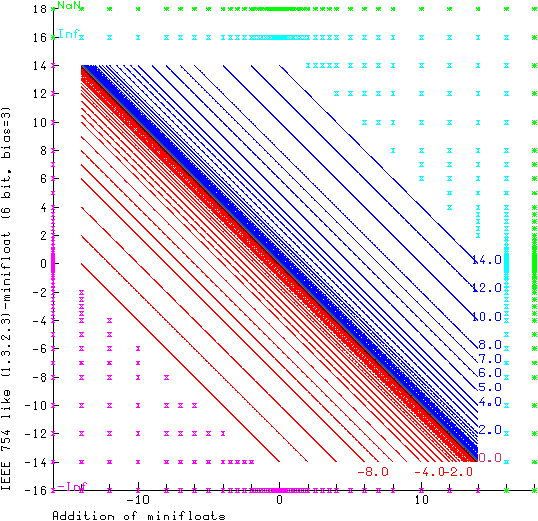 |
|---|
Додавання двох змінних FP6 формату s eee mm, з bias = 3. Зображення з вікі. У статті minifloat також є приклади для віднімання, множення та ділення. |
Vulkan визначає 10-бітни і 11-бітні типи, без біту знаку і з 5-бітною експонентою.
bfloat16 – 16-бітний тип, зручний для перетворення з float (FP32) – експонента та мантиса восьмибітні, тому для цього перетворення достатньо відкинути два байти FP32 – якщо підходить заокруглення із обрізанням. Тип std::bfloat16_t додано до С++23.
TensorFloat-32 від NVidia – 8-бітна експонента, 10-бітна мантиса, але сам тип займає 32 біти.
Спеціалізовані обчислювальні пристрої, такі як GPU, часто, заради продуктивності, ціною точності, не підтримують всіх вимог IEEE-754. Часто “відпадають” спеціальні та денормалізовані значення, правила заокруглення часто обмежені.
Жартівливі FP4 та FP3
Практична цінність таких крихітних типів, що реалізовують ідеї IEEE 754, нульова – якщо створювати їх для практичного використання, варто скористатися оптимізованим форматом, відмінним від описаного вище. Зокрема, не витрачати стільки значень на NaN. Однак, розглядати граничні випадки такого формату може бути повчально.
FP4, формат: s e mm
Для FP4 можна уявити два формати: однобітна експонента і двобітна мантиса та навпаки. Розпочнемо з першого випадку. Bias тут, як такий, відсутній – числа або денормалізовані, або спеціальні. Але для денормалізованих його беруть на 1 більшим, ніж “звичайни”, вважаючи, що bias може бути 0 або 1 – враховуючи можливі значення експоненти, то dn-bias – зсув денормалізованого числа, 1 або 2, але варіант із 0 – цікавіший.
| Двійкове | Десяткове, dn-bias=0 | Десяткове, dn-bias=1 | Десяткове, dn-bias=2 | Десяткове, dn-bias=-1 |
|---|---|---|---|---|
| 0 0 00 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0 0 01 | 0.25 | 0.125 | 0.0625 | 0.5 |
| 0 0 10 | 0.5 | 0.25 | 0.125 | 1.0 |
| 0 0 11 | 0.75 | 0.375 | 0.1875 | 1.5 |
| 0 1 00 | \(+\infty\) | \(+\infty\) | \(+\infty\) | \(+\infty\) |
| 0 1 01 | sNaN | sNaN | sNaN | sNaN |
| 0 1 10 | qNaN | qNaN | qNaN | qNaN |
| 0 1 11 | qNaN | qNaN | qNaN | qNaN |
| 1 0 00 | -0.0 | -0.0 | -0.0 | -0.0 |
| 1 0 01 | -0.25 | -0.125 | -0.0625 | -0.5 |
| 1 0 10 | -0.5 | -0.25 | -0.125 | -1.0 |
| 1 0 11 | -0.75 | -0.375 | -0.1875 | -1.5 |
| 1 1 00 | \(+\infty\) | \(+\infty\) | \(+\infty\) | \(+\infty\) |
| 1 1 01 | sNaN | sNaN | sNaN | sNaN |
| 1 1 10 | qNaN | qNaN | qNaN | qNaN |
| 1 1 11 | qNaN | qNaN | qNaN | qNaN |
Всі числа денормалізовані або спеціальні.
FP4, формат: s ee m
Оскільки множина значень експоненти вже не вироджена множина, розглянемо bias 0, 1, 2. Виглядає, що краще виходить, якщо dn-bias = bias32.
| Двійкове | Десяткове, bias=1 | Десяткове, bias=2 | Десяткове, bias=3 |
|---|---|---|---|
| 0 00 0 | 0.0 | 0.0 | 0.0 |
| 0 00 1 | 0.5 | 0.25 | 0.125 |
| 0 01 0 | 1.0 | 0.5 | 0.25 |
| 0 01 1 | 1.25 | 0.625 | 0.3125 |
| 0 10 0 | 2.0 | 1.0 | 0.5 |
| 0 10 1 | 2.5 | 1.25 | 0.625 |
| 0 11 0 | \(+\infty\) | \(+\infty\) | \(+\infty\) |
| 0 11 1 | qNaN | qNaN | qNaN |
| 0 00 0 | -0.0 | -0.0 | -0.0 |
| 0 00 1 | -0.5 | -0.25 | -0.125 |
| 0 01 0 | -1.0 | -0.5 | -0.25 |
| 0 01 1 | -1.25 | -0.625 | -0.3125 |
| 0 10 0 | -2.0 | -1.0 | -0.5 |
| 0 10 1 | -2.5 | -1.25 | -0.625 |
| 0 11 0 | \(-\infty\) | \(+\infty\) | \(+\infty\) |
| 0 11 1 | qNaN | qNaN | qNaN |
Виглядає, що такий тип, все ж, корисніший, ніж FP4 формату s e mm.
FP3
Менше, ніж три біти використати не вдасться – є три частини floating point. Отож, експонента і мантиса мають по одному біту. Dn-bias = -1, оскільки так веселіше.
| Двійкове | Десяткове |
|---|---|
| 0 0 0 | 0.0 |
| 0 0 1 | 1.0 |
| 0 1 0 | \(+\infty\) |
| 0 1 1 | qNaN |
| 1 0 0 | -0 |
| 1 0 1 | -1 |
| 1 1 0 | \(-\infty\) |
| 1 1 1 | qNaN |
Так би мовити, умовної корисності тип. :-) Зауважте також, bias не впливає на результат.
NaN-boxing
JavaScriptCore, Mozilla SpiderMonkey, LuaJIT використовують фокус – NaN-boxing.
- Змінні – 64-бітні.
- Floating point використовуються звично.
- А для всіх інших значень використовується NaN payload.
Огляд цього підходу: the secret life of NaN.
RISC-V використовує NaN-boxing так: для розширень із 64-бітними floating point, 32-бітні зберігаються у молодших 32-бітах відповідних регістрів, а старші біти дорівнюють 1 – завдяки цьому, завантаження 32-бітного числа як 64-бітне дасть NaN, корисне навантаження якого буде містити вихідне 32-бітне.
Історичні представлення
IBM 704
Згідно Вікі, це була перша масова машина із підтримкою floating point, схожих на розглянуті тут.
IBM 704 – ламповий мейнфрейм, випущений в 1954 році, виготовлено 123 екземпляри. Машинне слово – 36 біт, кожна машинна команда займала одне слово. Був здатен виконувати 12 тисяч додавань чисел з рухомою крапкою. FORTRAN та LISP були вперше розроблені для цього комп’ютера.
Формат чисел з рухомою крапкою займав машинне слово та використовував біт знаку, 8-бітову експоненту із зсувом 128, 27-бітну мантису.
 |
|---|
| Формат floating point чисел IBM 704, взято з документації. Зверніть увагу, що нумерація біт зворотня до використаної вище – звичної нам, MSB має номер 1, LSB – номер 35. |
Одиниця перед крапкою зберігалася явно, такі числа в документації називають нормалізованими. В ISA існують команди для нормалізованого (FAD – Floating Add) та не нормалізованого (UFA – Unnormalized Floating Add) додавання, віднімання (FSB, UFS), множення (FMP, UFM)33 та ділення (FDH – Floating Divide or Halt та FDP – Floating Divide or Proceed).
Також, в інструкції наводяться підпрограми для перетворення між fixed point та floating point і назад та ділення подвійної точності.
Ще однією цікавою особливістю цього комп’ютера була наявність індексного регістра.
Емулятор цього комп’ютера: Sim704.
IBM 7030 Stretch
Є в мене таке відчуття, що найбільш “хворенькі” ISA, архітектури, були в IBM…
Згідно Вікі, найшвидший суперкомп’ютер 1961-64 років.
Транзисторна машина, продано 9 одиниць. 64-бітовий процесор з паралельним ALU, до 16 мегабіт/256 кілослів34 RAM, продуктивність 1.2 MIPS. В цілому, виявилася помітно повільнішою машиною, ніж планувалося. Однак, хоча вважається невдалою, на ній відпрацьовувалося багато інновацій – конвеєр, попередня вибірка (prefetch) тощо.
Але найбільш цікаво не це:
- Команди 32-бітові або 64-бітові.
- Core-пам’ять зберігає 72-бітні слова, з яких використовуються програмно 64, а решта – “check bits”, які дозволяють випавляти однобітові помилки і виявляти всі двобітові.
- Адреси 18-бітові.
- Числа з фіксованою крапкою – змінної довжини.
- 1-64 біта двійкові та 1-16 цифр десяткові (у BCD форматі), беззнакові, або у форматі знак-модуль.
- При чому, ці 1-64-бітові значення могли перетинати границю слів core-пам’яті (RAM).
- Символи з кодами розміром 1-8 біт.
- Байти змінного розміру – 1-8 біт!
- Розмір даних задається в кодах операцій, явно чи неявно.
- Є своєрідні теги даних: знак комбінується разом з трьома ‘‘flag bits’’, цитую, “для ідентифікації чисел”, та 0-4 ‘‘zone bits’’, які – я тут навіть не візьмуся перекладати, “have no special function, but may be used as code bits to obtain an alphameric representation of the sign”.
- Zone bits йдуть ліворуч від sign, flag bits – праворуч, разом формуючи sign byte, розміром 1-8 біт, який теж задається в коді команди.
- Виглядає, що сам комп’ютер їх, окрім біту знаку, ніяк не інтерпретує. Однак, деякі команди переміщають їх в indicator register.
- Те, що ми б назвали регістрома прапорців, вони назвають indicator register.
- Таким чином, можна запрограмувати різну поведінку, в залежності від їх значень – такий собі поліморфізм.
- Акумулятор цікавий – 128+8-бітовий, має ліву 64-бітову частину, праву 64-бітову і ще, окремо, 8-бітовий регістр – знак акумулятора.
- Цитата щодо цієї акумулюторної ISA: ‘‘Universal accmulatos avoids misplacement of results’’.
 |
|---|
| Приклад формату цілочисельних даних з документації (стор. 17). Формат команд там ж, на на наступному рисунку, стор. 18. |
Floating point числа не настільки ‘‘варіабельні’’35, але формат незвичний:
- Ідея звична – є мантиса і експонента.
- Мантису в документації називають fraction bits.
- Вважається, що ліворуч від десяткової крапки – 0.
- Завжди починаються на границі слова RAM.
- В документації обговорюється, що це довзоляє швидкісну паралельну обробку36.
- 11 біт експоненти з окремим бітом її знаку, плюс біт EF – exponente flag.
- 48 біт ‘‘мантиси’’ – дробової частини.
- 4-бітовий байт знаку – знак і три прапорці, про які трішки було вище.
- В документації (стор. 82), наводиться приклад їх використання – позначати так крайні точки мешу (для якихось скінчених різниць).
- Тобто, розмір 61/64 біти37, які називають single precision, але є команди, які працюють з double precision – двома такими словами.
- Власне, напевне тому такий великий акумулятор.
- В single precision режимі, 60 біт зберігаються в лівій частині акумулятора, знак – у відповідному регістрі, молодша частина не використовуюється.
- Ремарка щодо читання документації: в термінах IBM, старший біт має номер 0 – на відміну від використованої нами нумерації, де 0 – молодший біт.
- В double precision – 60 бітів лівої частини ті ж, 48 старших бітів правої частини – друга половина мантиси.
- Таким чином, в double precision маємо своєрідний (96+12+1) = 109-бітовий тип.
- Коли EF == 0, експонента – від 0 до 1023.
- Коли ж EF != 0 – є два додаткових інтервали, XFP (exponent flag positive) – для додатньої експоненти, і XFN (exponent flag negative).
- Якщо я правильно зрозумів, XFP веде себе як безмежність, XFN – як нуль.
- Вони вважаються, цитуючи, “exceptional condition”. Див. також відповідну главу, стор. 83-84 документації.
- Є своєрідна нормалізація: числа бувають нормалізовані – 1 в старшому біті мантиси, і ненормалізовані (unnormalized).
- Виконувати чи ні нормалізацію, під час виконання команд, вказується відповідним бітом коду операції.
- Пост-нормалізація – нормалізація результату.
- Додавання і ділення використовують також пре-нормалізацію – нормалізацію аргументів.
- Біт коду команди вказує, вважати floating point (!) числа знаковими чи беззнаковими.
- Інший біт дозволяє змінювати знак результату на протилежний для множення, ділення та збереження в пам’ять і зміни додавання на віднімання.
- Заокруглення, як таке, не передбачено.
- В документації (стор. 81-82) пропонується, для коректного заокруглення виконувати double precision операції та команду “Store rounded” в кінці, яка заокругляє, додаючи 1 до 49-го біта результату, та зберігаючи 48 біт.
- Інтерпретація нуля там весела – їй ціла глава відділена (стор. 82-84).
- Є така цікава штука – Noisy mode.
- Під час нормалізації, якщо потрібно додати нові біти ліворуч, вони заповнюються нулями.
- Для перевірки, чи це не впливає надміру на результат, в noisy mode, біти праворуч заповнюються одиницями.
- Це дозволяє оцінити втрату точності в таких обчисленнях.
- Ціла колекція прапорців (індикаторів) для floating point, (стор. 85-86 та 164), наприклад “Preparatory Shift Greater than 48 (PSH)”.
 |
|---|
| Формат чисел з рухомою крапкою одинарної точності, з документації (стор. 17 та 78). |
Детальніше див.:
- IBM 7030 Data processing system: Reference manual
- IBM Stretch (7030) – Aggressive Uniprocessor Parallelism
- Стаття на вікі
ЕОМ “Київ”
ЕОМ “Київ” була розроблена в 1957-59 роках, існувало два екземпляри. Дуже цікава машина, але тут обмежимося лише згадкою про формат представлення чисел.
Машинне слово мало 41 біт. Формат команди включав 5 біт операцій та три адреси – двох джерел та результату.
Для представлення чисел використовувався fixed point формат – 1 біт знаку та 40 біт, які вважалися представленням числа від 0 до \(\frac {2^{40}-1} {2^{40}}\).
Існував від’ємний нуль, який викорисовувався деякими стандартними підпрограмами. Є всі основні арифметичні операції – додавання, додавання з переносом, віднімання, віднімання модулів, множення із заокругленням та без, ділення тощо.
Стандартна бібліотека підпрограм – вони були фізично “впаяні” (в документації так і називається, “постійно-спаяна пам’ять”), включала трансцендентні функції, такі як квадратний корінь чи \(1/2*\sin(x)\).
Для цього комп’ютера було реалізовано емулятор floating point.
Рання версія емулятора, розроблена студентками УКУ, знаходиться тут: Kyiv_emulator. В репозиторії є опис системи команд. Цікаві подробиці є також у презентації, а детальна табличка машинних команд – тут.
Посилання
Головні тексти
- IEEE Std 754-2019 (Revision of IEEE Std 754-2008). IEEE Standard for Floating-Point Arithmetic – поточна версія стандарту платна, але доступна в піратів.
- What every computer scientist should know about floating-point arithmetic by David Goldberg – дуже важлива стаття! Власне, в якомусь сенсі, цей текст є її переказом.
- What Every Programmer Should Know About Floating-Point Arithmetic or Why don’t my numbers add up? – зокрема, чому 0.1 + 0.2 не дорівнює 0.3. Зверніть увагу на меню ліворуч.
- Numerical recipes – Канонічний підручник по чисельним обчисленням. Старі версії доступні онлайн, нова версія, за певного старання знаходиться в Інтернеті. (Мушу зауважити, що С++ код останньої версії такий, не дуже С++ – С-з-класами, не більше, тому старішої версії, на С, має вистачати).
Додатково
Збірка різноманітних статей та есеїв, які стосуються тематики цієх глави.
- Numerical Computation Guide від Sun/Oracle.
- Floating Point Demystified, Part 1 та Part 2
- Зокрема, за мотивами – цікавий приклад: в Python, чи іншій мові, що працює із double:
0.1+0.2-0.3 = 5.551115123125783e-17.
- Зокрема, за мотивами – цікавий приклад: в Python, чи іншій мові, що працює із double:
- Floating-point error mitigation на Вікі.
- What Every Computer Scientist Should Know About Floating-Point Arithmetic
- Fast inverse square root – повчальний спосіб із коду Quake III Arena. В такому коді магічні константи типу 0x5F3759DF нікого не дивують.
- Understanding Quake’s Fast Inverse Square Root.
- Зокрема, ряд Тейлора сам по собі не дуже підходить – зазвичай, враховуючи скінчену кількість цифр, проблеми заокруглення тощо, можна запропонувати оптимальніші ряди.
- Hardware implementation of Denormalized Numbers by E. M. Schwarz et al.
- Logarithmic number system – альтернативний підхід до чисел з рухомою крапкою, що не набув популярності.
- Оптимізує множення та ділення, але ускладнює додавання та віднімання.
- IEEE 754 на вікі та посилання там.
- Accuracy of Mathematical Functions in Single, Double, Double Extended, and Quadruple Precision by Vincenzo Innocente and Paul Zimmermann, 2022
- Детальніше про підходи заокруглення і особливості різних способів, на Вікі.
- Сайт із цікавими статтями про floating point: Exploring Binary, містить ціле сімейство конвертерів:
- https://www.exploringbinary.com/topics/
- Decimal Precision of Binary Floating-Point Numbers – дискусія про кількість значущих цифр.
- The Spacing of Binary Floating-Point Numbers
- Decimal to Floating-Point Converter
- Base Converter
- Див. також конвертери на іншому сайті: Base Number - Decimal Number Conversion.
- Аудіокодек G.711, із цікавими маленькими floating point.
- FP64, FP32, FP16, BFLOAT16, TF32, and other members of the ZOO – лаконічний огляд.
- fp24fftk – 24-бітний float для FPGA
- Penalties of errors in SSE floating point calculations
- Dealing with Floating-point Exceptions in MSVC78 – цікава стаття, і хоча трохи застаріла, (більшою проблемою є те, що форматування прикладів порозповзалося).
- Floating Point and IEEE 754 Compliance for NVIDIA GPUs – гарний огляд.
- “Numerical computing with IEEE floating point arithmetic: including one theorem, one rule of thumb, and one hundred and one exercises” by Michael L. Overton, 2001
- Побавитися із стандартними floating point можна тут: Float Toy.
- Або тут: ieee754-visualization.
- Або тут: float.exposed.
- 0.1+0.3 різними мовами: 0.30000000000000004.com.
- Домашня сторінка William Kahan, творця IEEE 754.
- Decimal Arithmetic FAQ (Frequently Asked Questions)
- Random ASCII – tech blog of Bruce Dawson – велика кількість статей про нюанси floating point. На жаль, по тегу Floating point більшість із них не виводяться… Що цікаво, автор – розробник ігор і стикається із тим всім якраз в них. Обрані статті:
- Comparing Floating Point Numbers, 2012 Edition – в ній також є список попередніх статей за темою.
- Floating-Point Determinism – як досягнути побітової відтворюваності.
- Floating-point complexities – коротко про всілякі несподівані речі щодо формату.
- Exceptional Floating Point – про виключення в коді, з прикладами.
- That’s Not Normal–the Performance of Odd Floats – про втрату продуктивності від NaN, безмежностей, денормалізованих чисел тощо. Ремарка: якщо від заборони денормалізованих чисел код стає швидшим – ймовірно, він багато з ними працює, і від заборони помітно зміняться результати.
- Float Precision Revisited: Nine Digit Float Portability – про кількість цифр та “round-tripping”, збереження в текстову стрічку (файл) і назад.
- Intel Underestimates Error Bounds by 1.3 quintillion – одна із глав називається ‘‘Catastrophic cancellation, enshrined in silicon’’.
- How I joined the bug 323 community – про проблеми із 80-бітною точністю для 64-бітних типів.
- ARMv8 Instruction Set Overview.
- “Performance Degradation in the Presence of Subnormal Floating-Point Values”, 2005 – для паралельного коду, на прикладі Alpha i Intel x86. Конкретна інформація застаріла, звичайно, але застереження – ні.
- “Unum “ – цікава, але дискусійна спроба запропонувати альтернативний формат чисел з рухомою крапкою.
- “Floating Point Visually Explained”.
- “Whetstone Benchmark History and Results” – описано відповідний (застарілий) тест продуктивності floating point обчислень та його результати різних машин за тривалий час.
- “16-, 8- и 4-битные форматы чисел с плавающей запятой”.
- “Data Format and Conversion Information for Heritage Data at the National Space Science Data Center” – формат представлення різних даних комп’ютерами, що використовуювалися NASA, включаючи дуже старі машини.
- PDP-11 floating point
- CDC 1604 floating point – від’ємні числа зображаються оберненим кодом (ones’ complement).
- VAX Floating Point Numbers
- Додатково про VAX-формат – дискусія;
- dідповідь “Floating Point numbers on VAX machine” на stackoverflow;
- “VAX FLOATING POINT: A Solid Foundation For Numerical Computation” by Mary Payne and Dileep Bhandarkar, 1980.
- soft-ieee754 – бібліотека підтримки FP-чисел довільного розміру та довільним зсувом.
- “How to make sure no floating point code is used” – щодо embedded-систем.
- “Fuzzing floating point code”.
- “Herbie, the Numerical Compiler” – проект, який автоматично покращує точність floating-point коду, відповідним чином переформульовуючи формули. Зараз рухається в сторну врахування особливостей платформ.
- Алгоритм Кехена (Kahan summation),
- лема Штербенца (Sterbenz lemma).
- Array ordering and naive summation’’ – приклад, коли переставляння порядку підсумовування дозволяє отримати практично будь-який результат.
- '’Why are denormal floating-point values slower to handle?’’
- '’A calculator app? Anyone could make that’’ – цікавий есей про те, як зробити зручний і правильний калькулятор. Через особливості floating point і математичні властивості дійсних чисел, це нетривіально.
- '’Dragonbox’’ – реалізація швидкого нового (2018) алгоритму перетворення чисел у стрічку.
- ’‘The stack circuitry of the Intel 8087 floating point chip, reverse-engineered’’.
Виноски
-
В українській мові – з рухомою комою. Але про локалі ми будемо говорити окремо, тут користуємося формою, природнішою для більшості мов програмування. ↩
-
Будь-якого, із поширених, виду – float, double, long double, можна спробувати навіть “довгі”, із GMP, MPFR чи й MPC. ↩
-
Для уникнення дискусій, вважатимемо – істинно десятковий, який, як старі мейнфрейми IBM, зберігає числа в десятковому, а не двійковому, форматі. ↩
-
До прикладу, уявіть, що перша послідовність дій із прикладу – обчислення лівої сторони рівняння, а друга – правої. Запитання – чи вдалося розв’язати його? З точки зору такої машини – так, точніше вона просто не може38. ↩
-
Похибка, згідно відповідних правил, заокруглена до однієї значущої цифри, крім випадку, де вона величезна – заради наочності. ↩
-
Його використання не надає тих переваг, що є для операцій над цілими числами. ↩
-
Яка є константою – однаковою у всіх обчисленнях та вважається характеристикою реалізації відповідної підтримки чисел з рухомою крапкою – апаратної чи програмної. ↩
-
Така форма дозволяє, наприклад, порівняння двох floating point чисел виконувати як цілочисельну операцію (із врахуванням знаку та можливих NaN, але, все ж) – це на багатьох процесорах швидше. Щодо можливих нюансів – див., скажімо Stupid Float Tricks та лаконічний переказ. Також, разом із використаннями bias для представлення від’ємних експонент, завдяки такому порядку бітів, якщо інтерпретувати двійкове floating point як ціле число, додати до нього одиничку, то в floating point отримаємо наступне – більш далеке від нуля, представиме за допомогою цього запису дробове число. Перш ніж виконувати такі трюки на практиці, слід згадати про strict aliasing C/C++, який ми розглядаємо окремо. ↩
-
Як у відомому жарті: “1, 2, далі – багато”. ↩
-
Ким саме – обговоримо трохи пізніше. ↩
-
Від’ємні числа розташовані симетрично відносно нуля, не зображаємо для більшої виразності ілюстрації. ↩
-
Перейменували, як пояснюють, для більшої однозначності і зрозумілості, але подробиці я вияснити не зміг. ↩
-
Внаслідок цього, не всі 32-бітові цілі числа можна точно зберегти в 32-бітовий float, хоча інтервал його помітно більший, ніж максимальне 32-бітове ціле число. Те ж буде стосуватися 64-бітових цілих та binary64. ↩
-
Але, як дуже часто із типами цих мов, не гарантується. ↩
-
Окрім згадки на вікі статті “Crandall, Richard E.; Papadopoulos, Jason S. (2002-05-08). “Octuple-precision floating point on Apple G4 (archived copy on web.archive.org)”” ↩
-
Для лаконічності, далі не наводжу
std::numeric_limits<T>::. ↩ -
Оскільки поведінка деяких реалізацій може змінюватися під час виконання. ↩
-
Міжнародний стандарт ISO/IEC 60559:2020, тотожний за вмістом IEEE 754. ↩
-
Виглядає, що функції було використано, оскільки С++98 не вмів визначати не-цілочисельні константи. ↩
-
Точніше – ціле сімейство розширень. Важливо, що вони вміють працювати і в скалярному режимі – лише над одним операндом, тому можуть використовуватися і для “звичайних” обчислень з рухомою крапкою. ↩
-
Спочатку 8087 був співпроцесором, окремою мікросхемою, для 8086/8839, існували 80287, 80387 та купа екзотичних варіантів. Починаючи із 80486, інтегрований в процесор – його команди стали підмножиною системи команд процесора (ISA), але цей блок все ще часто називають x87. ↩
-
Зокрема, його GCC його використовує в 32-бітовому режимі. ↩
-
Проявивши певну настриливість, вдалося знайти, що Default NaN – такий, де знак нульовий, перший біт мантиси – 1, решта – нуль. ↩
-
Частково, оскільки біти порівняння чисел змінюються лише в режимі AArch32. В 64-бітнорму режимі використовуються “звичні” цілочисельні прапорці N-Z-C-V. ↩
-
Додатково, є, наприклад, Zfa – “Additional Floating-Point Instructions” чи L – “Standard Extension for Decimal Floating-Point”, які безпосередньо не стосуються нашої теми. ↩
-
Псевдокоманди – такі, що асемблером розгортаються у щось, відмінне від однієї команди – якусь послідовність абощо. ↩
-
Ці функції часто мають багато перевантажень і багато варіантів з іншими іменами. Наприклад, rintf(), rintl(), lrint(), тощо – кілька десятків. Їх не перераховуватиму, див. документацію за посиланнями. Тут зосереджуся на варіаціях у логіці заокруглення. ↩
-
Див. також math_errhandling. ↩
-
На жаль, якість та підтримуваність їх дуже відрізняється. Наприклад, з мого досвіду, uBLAS краще не використовувати. ↩
-
Тут обговорюємо лише дійкові fixed point, але, в загальному випадку, вони можуть бути десятковими чи й з іншою основою. BCD-представлення, яке підтримується деякими ISA, типу 32-бітних та старіших x86, можна використовувати для fixed point десяткової арифметики. ↩
-
Без цього, значення, що відповідають бінарному
0 00 1, потрібно ділити на два, і розподіл чисел біля 1 перестає бути рівномірним. ↩ -
Так, цей процесор мав множення та ділення! ↩
-
64-бітових. Так, це схоже на 2 мегабайти, звичних нам, але тут байтом називали не тільки 8-бітові послідовності, вирівняні на 8. ↩
-
Через них цей текст і з’явився – я шукав нетривіальні приклади представлення чисел з рухомою крапкою. ↩
-
Я зразу згадую вирівняні сучасні SIMD. ↩
-
64 біти в пам’яті, 61 – фактичний розмір ↩
-
Це, до речі, може спричиняти додаткові проблеми для наукових та інженерних обчислень. Уявіть, що дві кривих, \(f(x)\) та \(g(x)\) наближаються, але не торкаються – рівняння \(f(x) = g(x)\) фактично не має розв’язку. Однак, якщо віддаль менша за похибку, спричинену такими особливостями машинних чисел з рухомою крапкою, код може вирішити, що розв’язок існує. Для деяких задач, скажімо, теоретичної фізики – фазові переходи, все таке, це може бути важливим. ↩
